Nat. Commun. 2024 | $S O 3_{K R A T E S}$ : 利用欧几里得Transformer实现快速稳定的机器学习力场

今天介绍的是发表在 Nature Communications 上的一项工作 —— $S O 3_{K R A T E S}$ ：利用欧几里得Transformer实现快速稳定的机器学习力场。近年来，基于从头算参考数据训练的机器学习力场（MLFFs）在精度上取得了显著进展，但它们在长时间分子动力学（MD）模拟中的稳定性和效率问题仍备受关注。传统的SO(3)等变模型虽然在稳定性方面表现突出，却因昂贵的张量运算而受制于速度。 $S O 3_{K R A T E S}$ 提出了一种创新性的解决方案：通过欧几里得自注意力机制将不变与等变信息有效解耦，利用稀疏欧几里得变量表示分子几何，避免了高成本的张量积运算。该方法在精度、稳定性与速度三者之间实现了独特的平衡，相较现有等变架构可快至30倍，并能在数小时内完成纳秒级超分子动力学模拟。更重要的是，它不仅在训练数据内保持高精度，还能外推到未见过的构象，捕捉合理的低能结构。这一突破为大规模生物分子建模和新材料探索打开了新的可能性。

获取详情及资源:

论文: https://doi.org/10.1038/s41467-024-50620-6
代码: https://doi.org/10.5281/zenodo.11473653

0 摘要

近年来，基于从头算参考计算的机器学习力场(MLFFs)取得了显著进展。然而，尽管其在测试集上误差较低，MLFFs在分子动力学(MD)模拟中的可靠性正面临越来越多的质疑，主要原因在于长时间尺度下可能出现的不稳定性。研究结果表明，MLFFs的稳健性与等变表示的使用存在潜在关联，但这类表示的高昂计算成本在实践中限制了其优势。

为此，研究者提出了一种新的Transformer架构—— $S O 3_{K R A T E S}$ 。该方法结合了稀疏等变表示(欧几里得变量)与自注意力机制，将不变与等变信息有效分离，从而避免了对昂贵张量积运算的依赖。SO3KRATES在精度、稳定性与速度之间实现了独特平衡，使得对物质量子性质的深入分析能够在更长时间尺度和更大体系规模下进行。

作为验证，研究者生成了柔性肽段和包含数百原子的超分子结构的稳定MD轨迹，并进一步探索了中等规模链状分子(如小肽)的势能面拓扑，识别出数千个极小值。值得注意的是，SO3KRATES不仅能保持稳定性，还能够在训练数据之外发现新的低能构象，这对于生物化学中现实的结构探索任务至关重要。

1 引言

原子级建模依赖于长时间尺度的分子动力学(MD)模拟，以揭示实验上观测到的宏观性质如何由微观相互作用产生。这类模拟的预测精度取决于原子间相互作用力的准确性。传统上，这些力要么来自极度近似的经验力场(FF)，要么来自准确但计算代价极高的从头算电子结构计算。近年来，机器学习(ML)势能开始弥合这一鸿沟，它们利用分子体系中的统计依赖关系，展现出前所未有的灵活性。

通常，MLFFs的准确性由在少量基准数据集上的测试误差来衡量。然而，最新研究表明，测试误差与MLFFs在长时间MD模拟中的性能(真正的预测实用性标准)之间相关性很弱。只有准确的MD轨迹才能忠实表征动力学与热力学观测值。从ML角度看，这一缺陷源于外推性能不足，尤其在高温或柔性结构时，MD中探索的构型往往远离训练数据的分布。为改善这一问题，近年来涌现出一系列日益复杂的架构，其中消息传递神经网络(MPNNs)成为表现突出的代表。MPNNs可视为卷积在非结构化数据(如分子图)上的推广，能够有效提取输入特征。近期的进展集中在融入物理几何先验，催生了所谓的等变MPNNs，它们被发现能降低近似误差并提高数据效率。

不变模型依赖原子间的成对距离，但随着体系规模、柔性或化学异质性的增加，这种表征方式越来越难以准确描述相互作用模式。相比之下，等变模型能引入方向信息，捕捉依赖于相对取向的相互作用，从而学习更具可迁移性的相互作用模式。然而，等变架构的基本单元是张量积，它在卷积操作中计算两个函数的展开结果，导致函数空间维度呈指数增长。在SO(3)等变架构中，卷积在球谐函数基底上进行，为避免指数增长，通常限制球谐展开的最大角动量 $l_{m a x}$ 。尽管 $l_{m a x}$ 与精度和稳定性密切相关，但SO(3)卷积的计算复杂度随 $l_{m a x}^{6}$ 增长，使得预测速度较不变模型慢至多两个数量级。因此，实践中常需在精度、稳定性与速度之间妥协。

为解决这一问题，研究者提出了一种欧几里得自注意力机制，以原子邻域相对取向为滤波器来替代SO(3)卷积，从而无需昂贵的张量积。基于几何深度学习与神经网络设计的最新成果，提出了 $S O 3_{K R A T E S}$ 方法：它使用分子几何的稀疏表示，并将卷积响应投影到等变基底中最相关的不变分量。借助球谐函数的正交性，这一投影可简化为张量积的迹，等价于线性标度的内积，因而在保持高阶等变表示的同时，仍能高效扩展而不牺牲速度与内存。由此得到的不变能量模型，其梯度即为预测的力，天然具备等变性。整个过程中，自注意力机制用于在模型中解耦不变与等变基底元素。

与现有最先进的ML势能比较表明， $S O 3_{K R A T E S}$ 克服了等变MLFF的局限，在保持其优势的同时提升了速度和稳定性。该高效等变架构使得MD模拟稳定且快速，相较等变MPNNs可实现约30倍加速。研究者利用其在短短数小时内完成了超分子结构的纳秒级MD模拟，从小肽(42个原子)到纳米结构(370个原子)，并由此计算收敛的速度自相关函数傅里叶变换。此外， $S O 3_{K R A T E S}$ 还被用于探索二十二碳六烯酸(DHA)与Ac-Ala₃-NHMe的势能面拓扑，识别1万余个极小值。这一过程需要约3000万次力场评估，在100–1200 K范围内采样。若采用DFT方法，该分析需一年以上；现有等变MLFF需一个多月，而 $S O 3_{K R A T E S}$ 仅用2.5天即可完成，展现了实用时间尺度下探索大规模势能面的潜力。更重要的是，该模型还能识别出未在训练数据中出现的物理合理构象，这对于含丰富构象的大体系至关重要。

进一步的消融实验表明，等变性质与MD模拟的稳定性以及高温外推性能密切相关。即便在平均测试误差相同的情况下，等变表示仍能显著减小误差分布的扩展范围。引入方向信息的等变表示，与经典机器学习理论中“高维映射产生更丰富特征空间”的思想高度一致，使得模型更易于参数化和泛化。

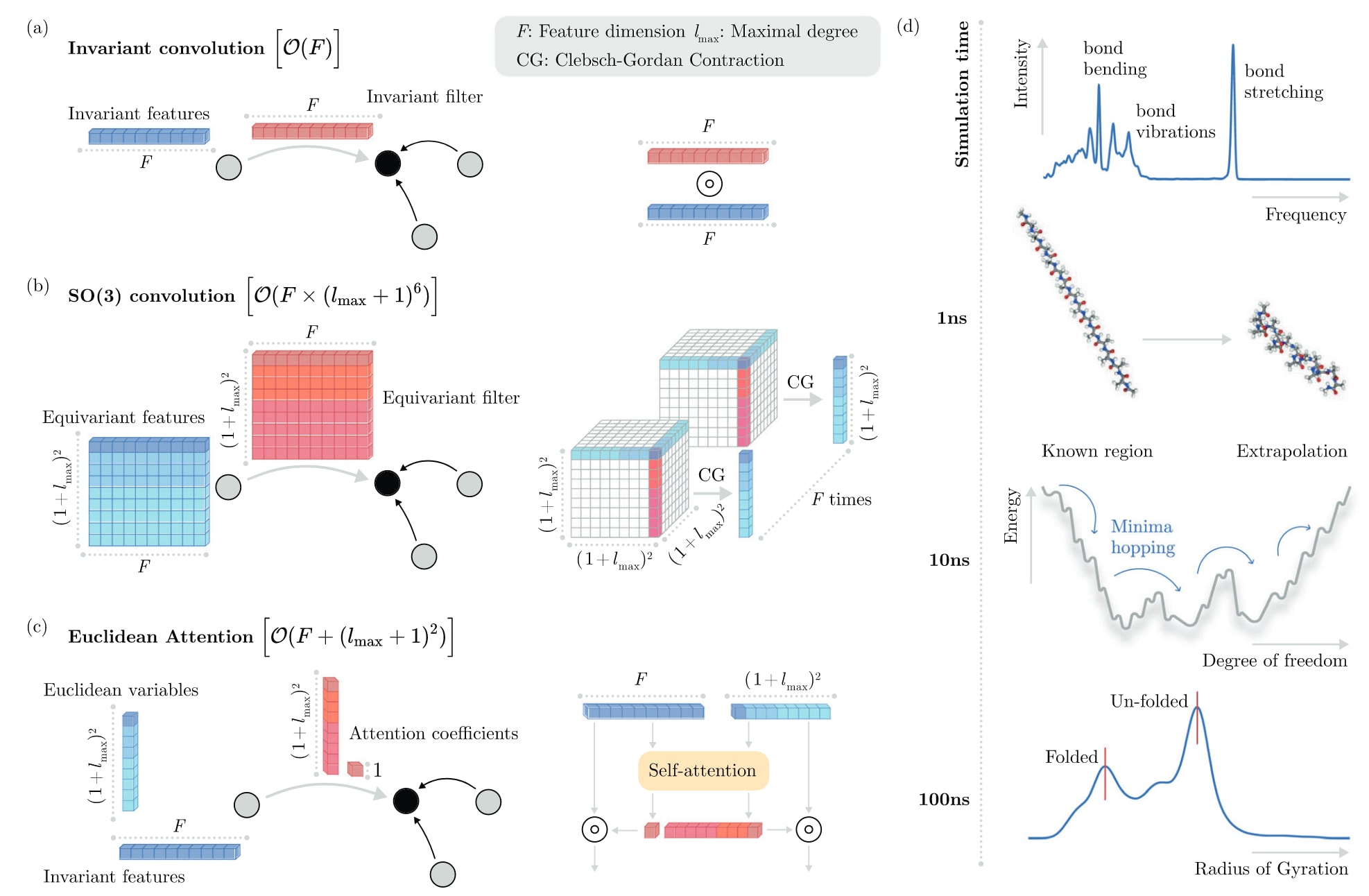
图1 | 结果概览。 a 不变卷积的示意图。b $S O (3)$ 卷积的示意图。c 支撑 $S O 3_{K R A T E S}$ Transformer的欧几里得注意力机制示意图。分子结构表征被分解为高维不变特征和等变欧几里得变量(EV)，二者通过自注意力机制交互。d $S O 3_{K R A T E S}$ 在稳定性与计算效率上的结合，使得其能够在不同模拟时间尺度上分析广泛性质(功率谱、折叠动力学、极小值分析、回转半径)。

2 结果

2.1 从等变消息传递神经网络到分离不变与等变结构： $S O 3_{K R A T E S}$

消息传递神经网络(MPNNs)继承了卷积的许多特性，能够作用于非结构化的输入域，例如欧几里得空间中的原子坐标集合。这使得它们成为描述势能面(PES)的一类有前景的方法，其中势能通常表示为：

E_{pot} ({\vec{r}}_{1}, \dots, {\vec{r}}_{n}) = \sum_{i = 1}^{n} E_{i} . (1)

这里，能量贡献 $E_{i} \in R$ 来源于高维的原子表征 $f_{i}^{(T)}$ 。这些表征通过迭代构建(共 $T$ 步)，其过程依赖于在原子邻域 $N (i)$ 内聚合成对消息 $m_{i j}$ ：

f_{i}^{(t + 1)} = UPD (f_{i}^{(t)}, {m_{i j}}_{j \in N (i)}), (2)

其中， $UPD (\cdot)$ 为更新函数，用于结合上一迭代的表征与聚合的消息。

在构建MPNN时，引入势能面的旋转不变性有两种常见方式。一种是基于不变输入(如原子间距离、角度或二面角)来构造消息，但这些输入集合往往是不完整的；另一种是采用SO(3)等变表示，在球谐函数等基底中进行系统性的多极展开，从而更好地匹配被建模体系的复杂性。

要将不变连续卷积的概念推广至 $S O (3)$ 旋转群，需要引入如下消息函数，其执行一次 $S O (3)$ 卷积可写为：

m_{i j}^{L M} = \sum_{l_{1} l_{2} m_{1} m_{2}} C_{l_{1} l_{2} L}^{m_{1} m_{2} M}, ϕ^{l_{1} l_{2} L} (r_{i j}), Y_{l_{1}}^{m_{1}} ({\hat{r}}_{i j}), f_{j}^{l_{2} m_{2}}, (3)

其中， $C_{l_{1} l_{2} L}^{m_{1} m_{2} M}$ 为Clebsch–Gordan系数， $Y_{l}^{m}$ 为 $l$ 阶 $m$ 次球谐函数， $ϕ^{l_{1} l_{2}} (r) \in R^{F}$ 调制径向部分， $f^{l_{2} m_{2}} j \in R^{F}$ 为原子特征向量。因此，执行一次卷积的复杂度为 $O (l^{6} max \times F)$ ，其中 $l_{max}$ 为网络中的最大阶数(图1b与图2)。

在此基础上，该研究提出两个对式(3)的概念性改动，统称为欧几里得自注意力(Euclidean self-attention)：

(1) 将消息分解为不变部分与等变部分；

(2) 使用基于不变输出的注意力函数替代 $S O (3)$ 卷积。

具体而言，首先从原子类型与邻域初始化原子特征 $f_{i}^{(t = 0)} \in R^{F}$ 与欧几里得变量(EV) $x_{i, L M}^{(t = 0)} \in R$ 。将所有阶数 $l$ 与次序 $m$ 的EV收集成单个向量，可得到维度为 $(l_{max} + 1)^{2}$ 的表征 $x_{i}$ ，其在旋转下保持等变性。

不变分量的消息表示为：

m_{i j} = α_{i j} f_{j}, (4)

等变分量的消息传播为：

m_{i j}^{L M} = α_{i j, L} Y_{L}^{M} ({\hat{r}}_{i j}), (5)

其中， $α_{i j} \in R$ 为逐阶注意力系数。聚合后的消息用于更新特征与EV：

f_{i}^{(t + 1)} = f^{(t)} i + \sum j \in N (i) m_{i j}, (6)

x_{i, L M}^{(t + 1)} = x_{i, L M}^{(t)} + \sum_{j \in N (i)} m_{i j}^{L M}, (7)

由于这种不变与等变的分离，整体消息计算的复杂度降为 $O (l_{max}^{2} + F)$ ，即将其他等变架构中的“特征维度与 $l_{max}$ 相乘”转化为“相加”(见表1)。

已有工作(如文献53)通过在等变边特征空间上迭代张量积，并引入一个不变潜在空间来实现类似的分离。而本文的方法则以原子级表征为核心，并在设计之初就将两类交互空间分开，从而完全避免了张量积运算。这两种设计选择都显著提升了计算效率。

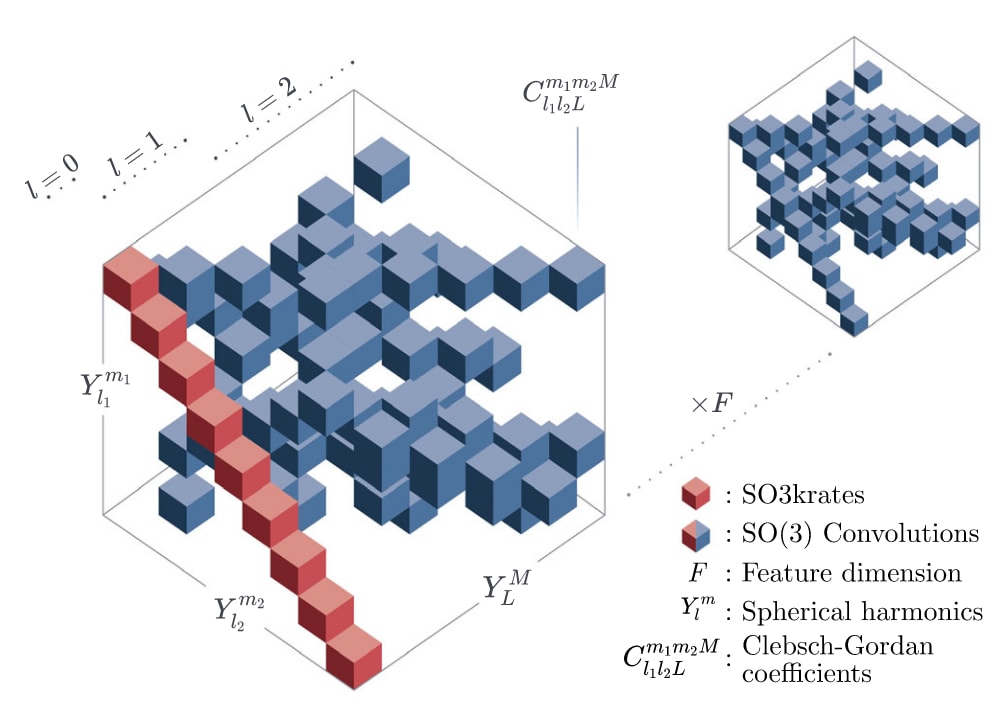
图2 | 基于不变量的学习。 $S O (3)$ 卷积在球谐基底中通过三重张量积构建，并在特征维度 $F$ 上重复 $F$ 次。本文将 $S O (3)$ 卷积替换为作用于不变量的参数化滤波函数(红色方块)，有效地将三重张量积约化为对简单张量积的逐度(trace)操作。彩色体元对应Clebsch–Gordan系数 $C_{l_{1} l_{2} L}^{m_{1} m_{2} M}$ 中的非零条目，用于掩码张量积。 $l$ 表示阶数， $Y_{l}^{m}$ 为球谐函数。

与其执行完整的 $S O (3)$ 卷积，本文将复杂相互作用模式的学习转移到一个注意力函数中：

α_{i j} = α (f_{i}, f_{j}, r_{i j}, x_{i j, l \leq l_{max}}^{l = 0}), (8)

其中， $x_{i j, l \leq l_{max}}^{l = 0}$ 是原子 $i$ 与 $j$ 的EV信号经过 $S O (3)$ 卷积后在 $l = 0$ 轴上的不变输出(详见“方法”IV B)。因此，式(8)能够非线性地融合原子邻域相对取向的信息。由于Clebsch–Gordan系数在 $l = 0$ 轴上是对角矩阵(图2)，计算不变投影仅需对长度为 $(2 l + 1)$ 的逐阶迹运算，其计算复杂度为 $O (l_{max}^{2})$ 。

在 $S O 3_{K R A T E S}$ 中，原子表征通过如下迭代过程不断优化：

f_{i}^{(t + 1)}, x_{i}^{(t + 1)} = ECTBLOCK ({f_{j}^{(t)}, x^{(t)} j, \vec{r} i j}_{j \in N (i)}), (9)

其中，每个欧几里得Transformer块(ECTBLOCK)由自注意力块与交互块组成。自注意力块实现了上一节描述的欧几里得自注意力机制；交互块则通过在同一原子上的特征与EV之间交换信息，提供了更多参数化自由度。

在经过 $T$ 次消息传递(MP)步骤后，最终的原子特征 $f_{i}^{(T)}$ 通过一个两层神经网络预测原子能量 $E_{i}$ ，并通过求和得到总势能(式(1))。原子力则通过自动微分获得，从而保证了能量守恒。

值得强调的是，所提出的等变架构并不局限于标量势能的建模，还可以推广至矢量与张量性质(如原子四极矩与八极矩)，其最高阶由设定的 $l_{max}$ 决定。例如，分子偶极可以通过将不变的部分电荷预测与 $l = 1$ 阶EV中提取的原子偶极相结合来学习。更为详细的架构组件说明与欧几里得自注意力框架的实现，见“方法”部分与图3。

表1 | 计算复杂度。

2.2 克服精度−稳定性−速度的权衡

下面的数值实验展示了 $S O 3_{K R A T E S}$ 如何克服分子动力学(MD)模拟中稳定性、精度与计算效率之间的权衡(图4)。近期一项研究比较了多种最先进MLFF在短时间MD模拟中的稳定性，发现只有基于 $S O (3)$ 卷积的NEQUIP架构能给出可靠结果。然而，这类模型的优异稳定性以高昂的计算代价为代价(图4a，上图)，因此需要在稳定性与计算效率之间做出妥协。而 $S O 3_{K R A T E S}$ 能够突破这一限制(图4b)。该模型的预测速度提升了约一个数量级的FPS(图4c)，使得步时达到亚毫秒级，同时在MD模拟中并未牺牲可靠性或精度(图4b)。

需要指出的是，测试精度与稳定性并不必然相关(如图4a中GEMNET与SPHERENET的对比)，只有同时具备高精度与高稳定性的模型才具备实际价值。结果表明， $S O 3_{K R A T E S}$ 在力预测中保持较高精度，从而有效克服了这一权衡(图4b)。在稳定性与速度方面，已有工作表明模型间存在精度−速度权衡(图4a，下图)，这一点与文献54的结论一致。

值得注意的是，运行时间的经验测量依赖于具体硬件与软件环境。文献32中报告的运行时间基于PYTORCH+ASE实现，而 $S O 3_{K R A T E S}$ 采用JAX实现。为保证公平性，研究者在相同的 $S O 3_{K R A T E S}$ 设置下，使用JAX重新实现了两类代表性模型：作为不变模型的SCHNET(速度上界)与基于 $S O (3)$ 卷积的NEQUIP(稳定性与精度最佳，复杂度下界)，并在相同GPU(Nvidia V100)与JAX-MD代码下进行测试。这一对照保证了后续比较在相同条件下进行。

结果表明，从PYTORCH+ASE(虚线)切换到JAX+JAX-MD(实线)可带来显著加速：NEQUIP提升28倍，SCHNET提升15倍(图4b)。这说明了统一实现环境的重要性，也体现了JAX生态的潜力。需要注意的是，这些步时不包含I/O操作时间，因为该部分高度依赖HPC环境，因此完整模拟的壁钟时间相较于报告的步时存在一个常量偏移。

在小有机分子(≤21个原子)体系中， $S O 3_{K R A T E S}$ 的平均速度较NEQUIP快约5倍，而步时比不变的SCHNET模型略慢(约1.4倍)。随着体系规模增大，相比 $S O (3)$ 卷积的加速倍数显著提升(图4c)，这与理论复杂度分析中更小的前因子一致(表1)。例如在双壁纳米管(370原子)体系中，相比NEQUIP的加速已提升至30倍。而与不变卷积相比， $S O 3_{K R A T E S}$ 预测速度略慢，这与理论分析结果相符。

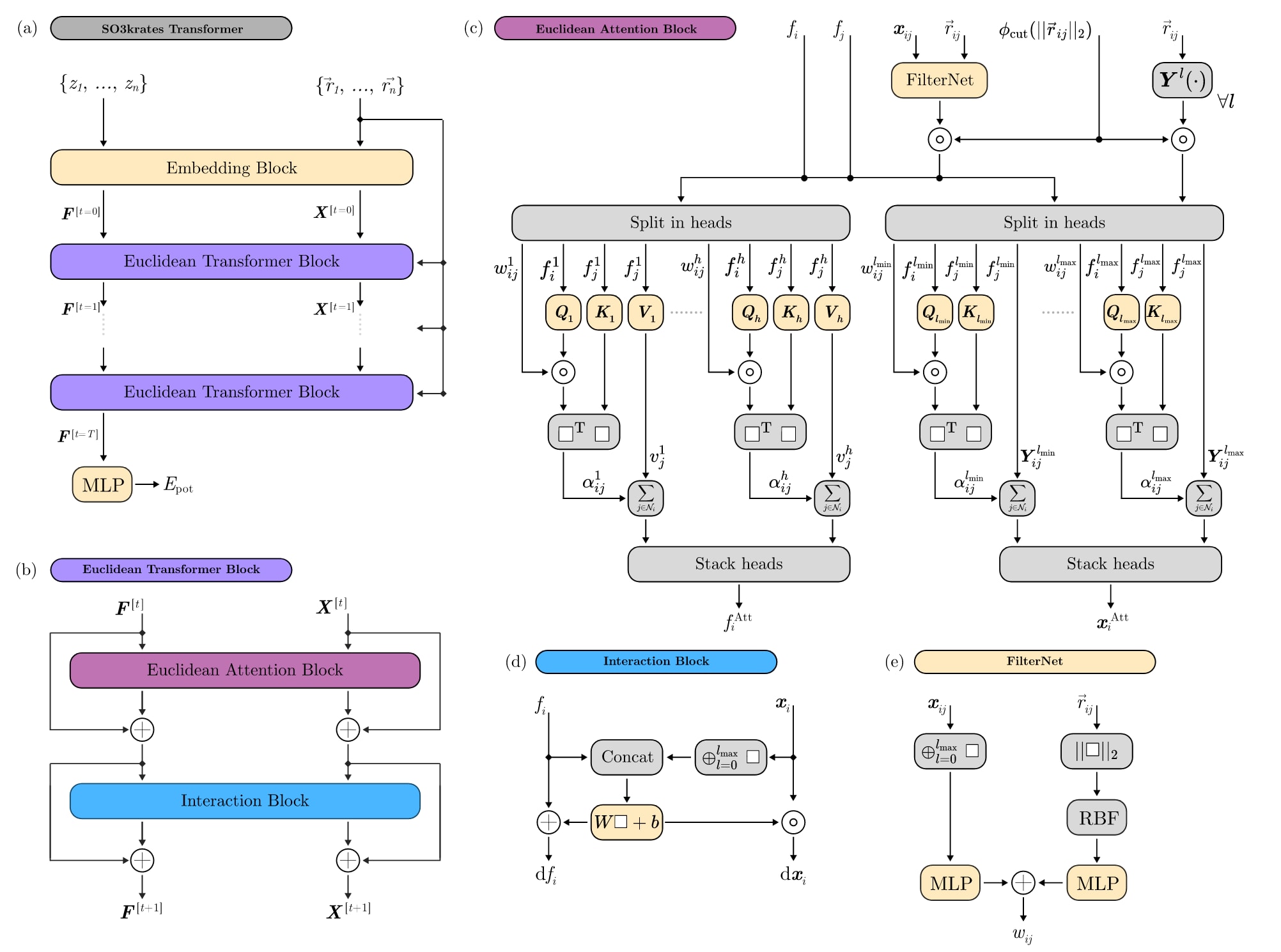
图3 | $S O 3_{K R A T E S}$ 的架构与构件。 a $S O 3_{K R A T E S}$ Transformer以原子类型 $Z = z_{1}, \dots, z_{n}$ 和原子位置 $R = {\vec{r}}_{1}, \dots, \vec{r} n$ 为输入，输出总能量 $E p o t$ 。在嵌入模块中， $Z$ 与 $R$ 被映射为不变特征 $F$ 与等变欧几里得变量(EV) $X$ ，并通过 $T$ 个欧几里得Transformer模块迭代优化。最终特征通过多层感知机(MLP)预测每个原子的能量并求和得到总能量。b 欧几里得Transformer模块由欧几里得注意力块与交互块组成，均带有跳跃连接以保留前层信息。c 欧几里得注意力块聚合原子邻域信息，分为更新不变特征与更新EV的两条分支。特征分支中，不变特征与滤波向量 $w_{i j}$ 被分为 $h$ 个注意力头。查询、键和值向量由特征通过可训练矩阵 $Q, K, V$ 得到。查询与滤波向量逐点相乘后与键向量点积，得到注意力系数 $α_{i j}$ ，用于加权邻域聚合。各头聚合的特征拼接得到单一特征 $f_{i}^{A t t}$ 。EV分支结构类似，但注意力头数由网络的最小阶 $l_{m i n}$ 与最大阶 $l_{m a x}$ 决定，值向量由球谐函数 $Y_{i j}^{l}$ 代替。d 交互块在特征与EV之间交换原子信息，将EV收缩为逐度不变量，并与不变特征拼接后经仿射变换得到更新。e 原子对位移向量被收缩为逐度不变量并送入MLP；同时，原子对距离展开为径向基函数输入MLP，输出的结果相加得到滤波向量 $w_{i j}$ 。

对于径向分布函数(RDF)，在四个研究体系的五次模拟运行中，结果均保持一致，并与DFT计算得到的RDF符合良好。值得注意的是，一些速度较快的MLFF模型在RDF预测上会出现明显偏差，其平均绝对误差(MAE)可达0.35(如水杨酸)至1.02(如萘)。相比之下， $S O 3_{K R A T E S}$ 的精度结果表明，高计算速度与从MD轨迹中获得精确物理量这一看似矛盾的需求可以兼得。

近期提出了一种严格局域的等变架构ALLEGRO，其优势在于并行化时无需额外通信，而MPNN在有 $T$ 层时并行化需要 $T - 1$ 次额外通信。以固体电解质Li₃PO₄为例，在192原子的晶胞上比较 $S O 3_{K R A T E S}$ 与ALLEGRO的精度与速度(图表2)。在推荐超参数下， $S O 3_{K R A T E S}$ 在能量与力的精度上比文献53报告的结果提升了超过50%，即便只使用了十分之一的训练数据。同时，在MD模拟中的计算速度仍保持相当。需要指出的是，文献53中的模型设定经过优化以追求速度而非精度，以展示可扩展性，这再次反映了精度−速度权衡，而 $S O 3_{K R A T E S}$ 在此基础上取得了改进。

为了进一步验证所得MD轨迹的物理合理性，还将 $S O 3_{K R A T E S}$ 在600 K下得到的RDF与DFT在Li₃PO₄淬火相中的结果进行了比较。结果显示， $S O 3_{K R A T E S}$ 不仅适用于分子体系，也适用于材料体系，展现出更广泛的适用性。

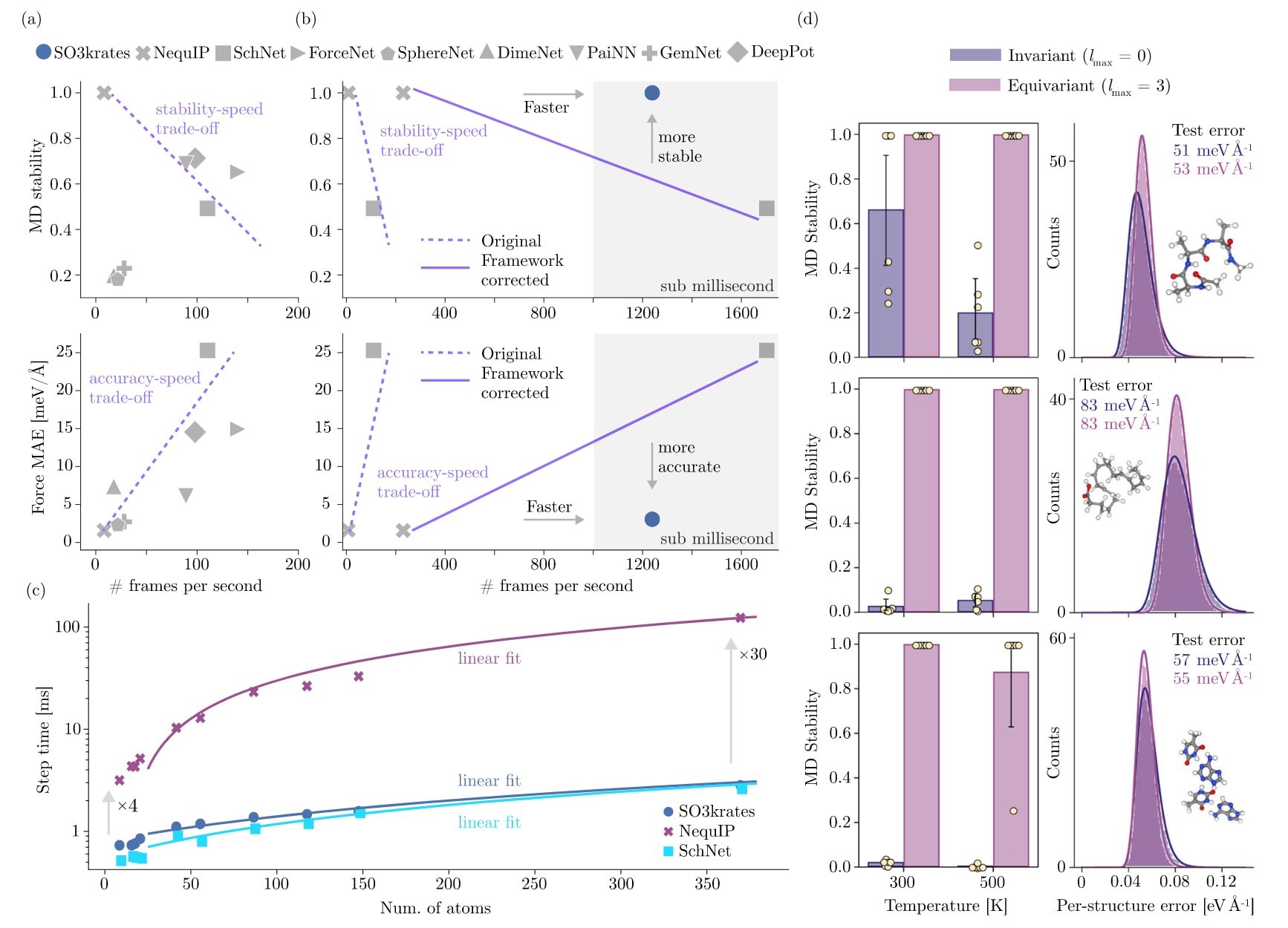
图4 | 计算效率与分子动力学(MD)稳定性。 a 每秒帧数(FPS)与平均稳定性系数(上图)及FPS与平均力MAE(下图)的关系，基于MD17数据集的4个小有机分子，比较不同最先进MPNN架构的结果。b 考虑硬件与软件实现差异，重新实现了两个代表性模型并在与 $S O 3_{K R A T E S}$ 相同的JAX设置下测试，得出框架校正后的FPS(虚线 vs 实线)。观察到NEQUIP加速28倍，SCHNET加速15倍。结果表明 $S O 3_{K R A T E S}$ 在保证精度与稳定性的同时不牺牲计算性能。灰色区域为步时低于1 ms的范围。c MD步时随体系原子数的变化。与 $S O (3)$ 卷积相比，较小的计算复杂度前因子带来体系规模增大时的显著加速。d 在300 K与500 K下的MD稳定性。升温导致不变模型稳定性下降，表明其外推能力较弱。像DHA这样柔性的分子在300 K下已对不变模型构成挑战。柱高为6次MD运行的平均稳定性，黄色点为单次运行结果，误差棒为2σ置信区间。补充表1给出了具有相同测试误差的不变与等变 $S O 3_{K R A T E S}$ 模型的逐结构误差分布。

表2 | 周期性体系的精度与速度。

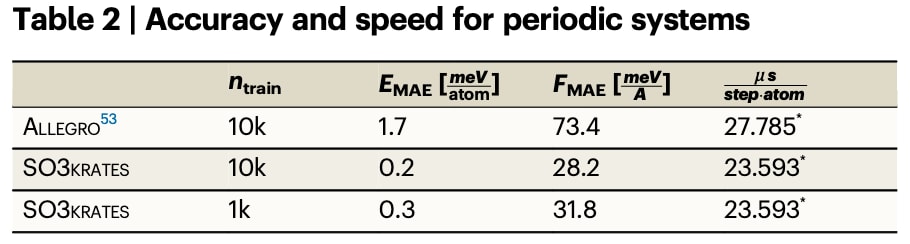
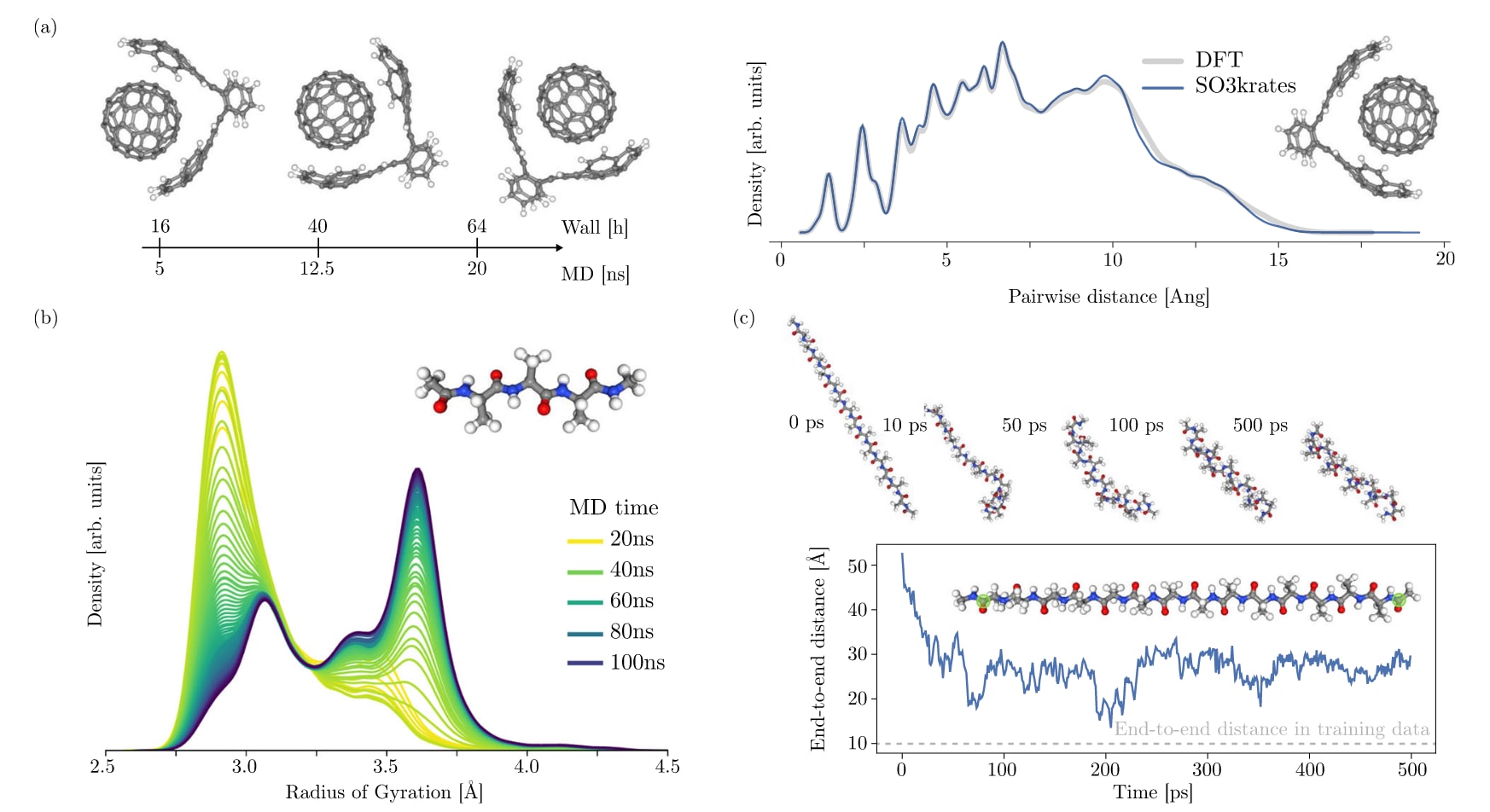
图5 | 稳定的长时间尺度分子动力学模拟与大分子外推。 a $S O 3_{K R A T E S}$ 的稳定性与速度使得超分子结构的纳秒级MD模拟在数小时内完成。例如在20 ns模拟中，富勒烯捕手结构保持完整，说明模型正确捕捉到弱非共价相互作用。b Ac-Ala₃-NHMe在20 ns步长下的回转半径(ROG)分布，60–80 ns后收敛，凸显稳定且高效模拟的重要性。c 使用仅1k个小肽(Ac-Ala₃-NHMe)数据点训练的模型模拟Ala₁₅的动力学，末端距分析显示其快速折叠为螺旋结构，说明局域表征具备推广至更长尺度构象变化的能力。

2.3 数据效率、稳定性与外推性

数据效率和分子动力学（MD）稳定性在机器学习力场（MLFFs）的适用性中起着关键作用。高数据效率意味着即使在数据量有限的情况下，也能获得准确的势能面（PES）近似，这是常见情形，因为量子力学从头算方法计算量极其庞大。即便能获得很高的精度，如果缺乏MD稳定性，也无法从轨迹中计算出可靠的物理观测量。

在此，研究者展示了通过增加网络中的最大角动量阶数 $l_{m a x}$ ， $S O 3_{K R A T E S}$ 的数据效率能够进一步提升。研究者还发现，MLFF的稳定性与向高温外推的能力可以与等变表示的引入相关联，而这一点与测试误差估计值无关（图4d）。为理解方向信息的益处，研究者比较了一个等变模型（ $l_{m a x} = 3$ ）与一个不变模型（ $l_{m a x} = 0$ ）。由于使用了多头注意力机制，从 $l_{m a x} = 0$ 提升到 $l_{m a x} = 3$ 时，网络参数数量变化可以忽略不计（方法，第IV H节）。所有模型均在11k个随机采样的构型上训练，其中1k用于验证。对于不变模型，只有在这种训练规模下，才能将力误差降低到接近 1 kcal·mol⁻¹·Å⁻¹。由于等变表示提升了ML势能的数据效率【24,36】，研究者预计在相同训练样本下，等变模型会有更低的测试误差。以DHA分子为例，这一预期得到验证（补充图4）。

为了公平比较不变与等变模型，研究者将不变模型训练到验证误差收敛，再将等变模型训练至相同验证误差，结果在测试集上得到相同平均误差（图4d和补充表1）。然而，由于等变模型更高效地利用了训练数据，它只需要不变模型约1/5的训练步数即可达到相同验证误差（补充图4d）。

接着研究者比较了测试误差的分布，因为相同的平均值并不代表分布特征一致。以逐原子力误差 $ε_{i} = ‖ {\vec{F}}_{i}^{p r e d} - {\vec{F}}_{i}^{r e f} ‖_{2}$ 为例，结果显示两类模型的误差分布在性质上相似，只在高度和宽度上略有差异（补充图5b）。但在逐结构的力误差 $R_{i} = \frac{1}{| S |} \sum_{i \in S} ε_{i}$ 的分布上，差异明显（图4d）：不变模型在某些构象上表现得更好（甚至优于等变模型），但代价是在其他构象上的表现更差，这一点在逐原子误差中是不可见的。

稳定性系数（公式28）来自六次300 ps的MD模拟，步长0.5 fs，温度 $T = 300$ K 与 $T = 500$ K（图4d）。结果表明，不变模型在最小且柔性最低的结构AcAla₃-NHMe上表现最佳，但在高温下稳定性明显下降。温度升高意味着轨迹中更频繁地出现训练数据未覆盖的构象，因此需要更好的外推能力。在柔性较大的体系（如DHA，图4d第二行）中，不变模型已无法维持稳定的MD模拟。为排除不稳定性源于 $S O 3_{K R A T E S}$ 本身的可能性，研究者还训练了一个SCHNET模型，其MD稳定性与不变的 $S O 3_{K R A T E S}$ 模型相当。因此，方向信息对学习到的能量流形的影响超越了精度和数据效率。

腺嘌呤−胸腺嘧啶（AT-AT）复合物则是一个微妙的案例。等变模型在500 K下的六次模拟中有一次出现不稳定，说明等变模型的稳定性提升应被理解为降低失效概率，而非绝对保证。研究者强调，对于任何经验模型而言，意外行为都不能完全排除。在AT-AT复合物的模拟中，还观察到子结构（A、T或AT）解离（补充图6）。这种行为对应于氢键或π–π相互作用的断裂，突显了弱相互作用对MLFFs的挑战。有趣的是，对于其他超分子体系，非共价相互作用则得到了正确描述（第II F节，图5a）。需要指出的是，AT-AT的训练数据仅来自一条20 ps的从头算MD轨迹，仅覆盖了所有可能构象的一小部分，因此很容易离开数据流形。结果表现为，当模拟温度升高时，解离速率增加，因为每单位模拟时间内可达构象空间被有效扩展。

表3 | MD22基准性能。

2.4 回转半径

回转半径（ROG）是表征聚合物结构与动力学行为的重要观测量，它能够用于评估蛋白质的结构紧凑性，并且可以通过实验获得。结构变化的时间尺度通常在几十纳秒甚至上百纳秒，这意味着需要相当长度的模拟才能获得收敛的ROG分布。因此，机器学习力场（MLFF）必须既稳定又高效，能够支撑数百纳秒的动力学模拟。本文展示了 $S O 3_{K R A T E S}$ 在该类应用中的潜力：利用其在300 K下进行100 ns的MD模拟，从而得到Ac-Ala₃-NHMe的收敛ROG分布（图5b）。在步长为0.5 fs时，该模拟需约2亿次力评估，而 $S O 3_{K R A T E S}$ 能在单张A100 GPU上仅用5天完成。对不同时间段的ROG分布进行分析发现，达到收敛确实需要如此长的时间尺度，且分布中出现了特征峰，分别对应折叠与未折叠的构象。

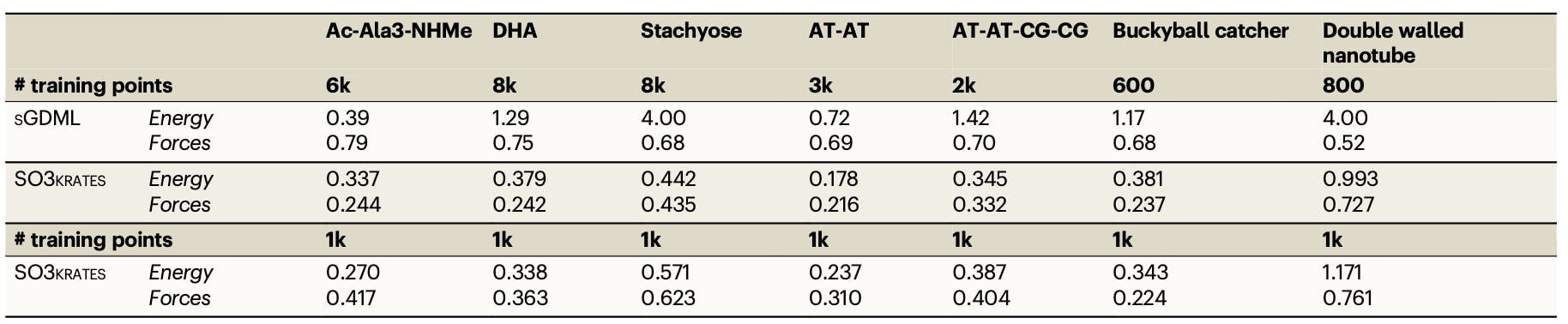
2.5 向更大肽链的推广

将MLFF推广至更大结构和未知构象是生物化学真实模拟中不可避免的需求。结果表明，即使仅使用一个小肽（42个原子）的1000个训练点， $S O 3_{K R A T E S}$ 也能推广到更大肽链（151个原子），且无需额外训练数据。尽管模型具有局域性，仍能观察到其自发折叠为螺旋结构，体现了所学表示的外推能力。进一步，将训练于Ac-Ala₃-NHMe的模型直接应用于Ala₁₅，从延展构象出发（图5c左），分析首残基与末残基羰基碳之间的端到端距离（绿色球所示）后发现，该肽链能够快速折叠为二级螺旋结构（图5c右）。与Ac-Ala₃-NHMe的端到端距离（灰色虚线）相比， $S O 3_{K R A T E S}$ 展示了对超出训练数据尺度的构象变化的泛化能力。

2.6 功率谱

原子速度功率谱是连接MD模拟与实验数据的重要工具，它通过速度自相关函数的傅里叶变换获得，适用于从小肽到主客体体系及纳米结构的研究。要正确描述这些体系，模型必须能够同时捕捉共价与非共价作用。在最大规模370个原子的体系上， $S O 3_{K R A T E S}$ 运行500万步MD仅需20小时（约15 ms/步）。研究者在MD22数据集中为每个结构训练独立模型，并与SGDML进行对比（表3）。采用两种训练集规模：(A) 每个结构使用600至8000个样本（文献61方案）；(B) 每个结构统一使用1000个样本，以评估在有限数据下的表现。结果表明，即使在(B)设置下，测试集上的力误差也低于1 kcal·mol⁻¹·Å⁻¹，且整体精度优于SGDML。

利用 $S O 3_{K R A T E S}$ 进行1 ns的MD模拟，进一步计算功率谱并与实验红外光谱对比。在buck球捕手和双壁纳米管体系中（图6a），均能观察到C–C振动（500与1500 cm⁻¹）、C–H弯曲（约900 cm⁻¹）及C–H伸缩（约3000 cm⁻¹）的显著峰值，且正确再现了范德华相互作用对双壁纳米管相对旋转自由度的贡献。对于DHA分子，功率谱随温度发生非平凡的位移（图6b），揭示了模型能够学习势能面的非谐贡献。进一步结合零点能（ZPE=12.979 eV，对应930 K）分析表明，即使模拟温度接近训练温度的两倍，动力学仍保持稳定，凸显了方法在高温条件下的适用性。

2.7 势能面拓扑

构象变化的准确描述是分子生物物理学中最具挑战的问题之一。每一种构象对应势能面上的一个局域极小值，而极小值数量随体系规模呈指数增长，极大限制了从头算方法或昂贵MLFF的适用性。本研究在DHA与Ac-Ala₃-NHMe上探索了1万个极小值，每次模拟需约3000万次力场评估。若使用DFT需逾一年，现有等变架构亦需一月以上，而 $S O 3_{K R A T E S}$ 仅用2天完成。

通过最小化跃迁算法（minima hopping），研究者构建了DHA的断连图（disconnectivity graph），发现其势能面存在多个由能垒隔开的折叠漏斗，最高能垒达3 eV（补充图12）。对于Ac-Ala₃-NHMe，通过Ramachandran图（图6d,e）可视化访问到的1万个极小值位置，结果显示 $S O 3_{K R A T E S}$ 能够探索训练数据之外的新区域，表明其具备外推能力。对比所选四个高密度区域的极小值与DFT计算，能量平均偏差仅3.45 meV，其中位于未采样区域的一个极小值仅偏差0.7 meV，显示出高度一致性（图6f）。尽管部分极小值（如C）在与DFT的对比中出现更大偏差（41.84 meV），但整体结果验证了 $S O 3_{K R A T E S}$ 在捕捉构象能量学与主链二面角分布方面的可靠性。

图6 | 功率谱与势能面(PES)极小值探索。 a 富勒烯捕手(上)与双壁纳米管(下)的功率谱，由速度自相关函数的傅里叶变换计算。b DHA在零点能与500 K下的功率谱，并与简谐近似对比。c 对DHA进行极小值搜索，共访问1万极小值，对应约2000万步MD逃逸与1000万次PES松弛。右侧展示最高能量、最低能量与中间能量的代表极小值。d Ac-Ala₃-NHMe的Ramachandran密度图：上为训练构象，下为极小值搜索访问到的构象，黄色点为实际访问点。部分极小值未出现在训练数据中，说明模型具备发现新极小值的能力。e Ac-Ala₃-NHMe结构及主链角度示意。f Ramachandran图中四个高频区域(A–D)的极小值能量比较，结果对比了 $S O 3_{K R A T E S}$ 能量、DFT单点能量及DFT松弛能量。g 训练外极小值与DFT松弛极小值在Ramachandran图中的位置。

3 讨论

长时间尺度的分子动力学（MD）模拟对于揭示分子体系的收敛动力学和热力学观测量至关重要。然而，尽管许多最新的机器学习力场（MLFFs）在测试集上表现出较低误差，它们在长时间模拟中仍可能出现不可预测的行为，这是由于输出中非物理贡献的积累所致，从而使得在长时间尺度上获得稳定结果变得极其困难甚至不可能。这直接阻碍了对大规模体系中物理可信观测量的提取。

现有研究尝试通过引入物理上有意义的对称性约束来提升稳定性，但其高昂的计算成本削弱了方法在实践中的优势。研究者提出的 $S O 3_{K R A T E S}$ 体系，通过结合欧几里得自注意力机制与欧几里得变量（EV）表示，在等变Transformer架构中实现了稳定性与效率之间的平衡。其卓越性能源于不变特征与等变特征的解耦，这大幅降低了计算复杂度，同时有效利用了计算资源。

在模型设计上，研究者让计算代价低廉的不变部分（ $l = 0$ ）使用更多参数，而高成本的等变部分（ $l > 0$ ）则受到严格约束。即便如此，等变模型所带来的优势仍得以保留，包括高数据效率、可靠的MD稳定性以及温度外推能力。在实际模拟中，研究者发现等变网络（ $l_{max} > 0$ ）的力误差分布更窄，在结构层面上比不变网络（ $l_{max} = 0$ ）表现更稳定，而不变模型往往对部分构象过拟合。随着温度升高，不变模型稳定性迅速下降，而等变模型则表现出更好的外推能力。

将 $S O 3_{K R A T E S}$ 应用于MD22基准中的不同结构（如小肽Ac-Ala₃-NHMe、DHA，以及超分子结构AT-AT、buck球捕手和双壁纳米管），研究者能够实现稳定且跨越数十纳秒/天的MD模拟。这使得诸如功率谱、ROG收敛分布等实验相关观测量的计算成为可能。研究者还展示了其在小分子中的构象变化预测能力，能够识别训练数据中未出现的物理合理极小值。例如，Ac-Ala₃-NHMe的代表性表明，该方法有潜力推广至更大肽链与蛋白质。由于从头算数据在这一尺度上的稀缺性，势能面（PES）的外推能力是实现大规模生物分子建模的关键。

近期也有一些工作提出了简化SO(3)卷积计算复杂度的方法，它们通常作为替代模块嵌入到现有框架中。而研究者的方法则完全避免了昂贵的SO(3)卷积操作，从根本上提升了效率。这表明等变相互作用优化仍是一个活跃且未成熟的研究方向，未来仍有进一步改进空间。

尽管 $S O 3_{K R A T E S}$ 使得在现代MLFF范式下实现稳定的长时间模拟成为可能，要让其在应用性上接近传统经验力场，仍需进一步努力。未来有几条值得探索的方向：

多体展开：当前EV仅基于两体相互作用，而引入原子簇展开可能进一步提升精度，同时减少消息传递步数、降低计算复杂度。
全局效应建模：如何合理处理长程效应仍在讨论中。已有尝试包括低秩近似、可训练的Ewald求和，或在物理启发下学习长程修正。这些方法对于大体系外推尤为重要。
与局域描述子的集成：许多长程修正依赖于局域属性（如部分电荷、电负性或Hirshfeld体积），它们可以自然地嵌入到 $S O 3_{K R A T E S}$ 的不变特征分支中。

未来的工作将聚焦于将多体展开、全局效应与长程相互作用纳入EV形式主义中，同时进一步提升计算效率，从而最终在高精度下跨越更长的MD时间尺度。

Nat. Commun. 2024 | SO3KRATES: 利用欧几里得Transformer实现快速稳定的机器学习力场