NC 2023 | VisNet: 基于等变向量–标量交互消息传递的分子几何表示增强方法

今天介绍的这项工作来自 Nature Communications。近年来几何深度学习在分子建模领域引起了显著关注。随着等变图神经网络的发展，模型在预测分子能量、力以及量子化学性质方面逐渐逼近从头算的精度。然而，这类模型在实际应用中仍面临两类主要挑战：一类是对几何信息的利用不足，导致模型难以充分捕捉分子结构中的关键空间关系；另一类则是高阶几何张量计算成本过高，使得模型难以扩展到更大、更复杂的分子体系。针对这些技术瓶颈，一种称为ViSNet的等变几何增强图神经网络方法被提出。该方法的核心在于设计了运行时几何计算策略，通过向量表示隐式获取角度、二面角和不正确扭转角等多类几何信息，使计算复杂度从常见显式方法的 $O (N^{2})$ 或 $O (N^{3})$ 降至线性级别。与此同时，模型还利用球谐函数延展向量表征，但以内积替代高成本的Clebsch–Gordan积，从而避免高阶群表示中常见的计算瓶颈。在此基础上，向量与标量之间的交互式消息传递机制进一步强化了模型在几何表征方面的能力，使节点特征与边特征都能在更新中融入丰富的空间信息。通过大规模基准测试可见，该方法在多种分子动力学数据集上取得了领先的能量与力预测精度，并在QM9、Molecule3D等量子化学数据集中展现出优异的性质预测能力。除了在数据集上表现优异，ViSNet还展示出在分子动力学模拟中的潜力。使用少量训练样本时，仍能逼近从头算在构象空间探索中的表现，显示出良好的数据效率和高保真度。实际应用中，对于复杂体系如166原子的Chignolin蛋白，模型在能量和力的预测上也表现稳健，甚至可与经验力场相比显著改进精度。这说明该方法不仅能够处理小分子，也具备向更大体系扩展的能力。从整体来看，这项研究展示了如何在保持可扩展性的同时有效利用高阶几何信息，为分子建模与分子动力学模拟提供了一个兼具精度与效率的解决方案。ViSNet的设计思路也凸显了向量与标量信息交互的重要性，为未来的几何深度学习模型提供了新的方向。

获取详情及资源:

📄 论文: https://www.nature.com/articles/s41467-023-43720-2
💻 代码: https://github.com/microsoft/AI2BMD/tree/ViSNet

0 摘要

几何深度学习正持续推动分子建模领域的革新。尽管当前的神经网络模型在分子性质预测方面已逐渐逼近从头算精度，其在药物发现与分子动力学模拟等应用中的表现仍受到两类因素的限制：一是对几何信息的利用仍不充分，二是高计算成本带来的效率瓶颈。针对这些问题，一种名为ViSNet的等变几何增强图神经网络被提出。该方法能够以低计算开销有效提取几何特征，并对分子结构进行高效建模。ViSNet在多个分子动力学基准上表现优于已有方法，包括MD17、修订版MD17和MD22，并在QM9与Molecule3D数据集上展现出优异的化学性质预测能力。此外，通过一系列模拟与案例研究，ViSNet能够高效探索分子构象空间，并能在几何表征与分子结构之间提供合理的可解释性。

1 引言

分子建模在当代科学与工程领域中具有重要地位，有助于理解化学反应、推动新药研发，并促进科学与技术的发展。密度泛函理论是分子建模中常用的方法之一，能够精确计算分子的能量、力以及其他化学性质。然而，由于其计算需求极高，特别是在处理大规模分子体系或高精度计算时，常常需要大量计算资源与时间。机器学习提供了另一种选择，通过从参考数据中学习以接近从头算的精度，同时具有更高的计算效率。梯度域机器学习方法利用能量守恒与从头算分子动力学轨迹中的有限样本构建精确的分子力场，使得在保证精度的前提下实现高效模拟。其后基于对称性的扩展进一步将物理对称性引入力场构建，使结果能够达到处理柔性分子的高精度水准。迭代式的扩展方法又将这一思路推广到包含数百原子的体系，能够保持原子间关联并准确描述复杂分子与材料。

近年来，深度学习因其能从原始数据中自动学习特征而备受关注，但其对大量数据的依赖成为在更多场景中应用的限制。为了缓解深度学习势能模型对数据的依赖，一些研究将对称性的归纳偏置引入神经网络设计，形成几何深度学习的方向。对称性描述物理规律在平移与旋转等变换下保持不变，使得相关模型能够在有限数据场景中无需数据增强即可学习稳定的表示。

在几何深度学习框架中，等变图神经网络是一类重要方法，具备强大的分子几何建模能力。一类常见方法通过方向信息实现等变性，并将几何特征用于预测分子性质。例如，某些模型在已有的结构上加入二面角信息，通过显式的几何张量提取欧氏空间中的几何关系；也有方法采用向量嵌入并通过向量自身的内积隐式处理角度信息，从而降低显式几何提取的复杂度。另一类主流方法借助群表示论实现等变性，能达到更高精度，但计算成本相当高。这类方法利用高阶几何张量，在多个分子动力学数据集上获得领先性能，但由于需要计算繁重的Clebsch–Gordan积，虽然适用于具有周期性的系统与精心设计的模型结构，却难以在大规模非周期分子体系（如化学或生物分子）中实际应用。

针对计算成本与几何信息利用不足之间的矛盾，该研究提出ViSNet，即“Vector-Scalar interactive graph neural Network”。该方法通过运行时几何计算策略以线性时间隐式提取多种几何特征，包括角度、二面角与不正确扭转角，符合经典分子动力学力场中的几何构成，从而显著加速训练与推理并降低内存消耗。同时，为了扩展向量表示，模型引入球谐函数，并以内积取代计算代价高昂的Clebsch–Gordan积。进一步地，精心设计的向量–标量交互式等变消息传递机制能够在向量与标量表征之间高效交换几何信息，使模型能够充分利用结构中的空间信息。

在多个基准数据集的综合评估中，ViSNet在MD17、修订版MD17与MD22上的所有分子均优于现有方法，并在QM9与Molecule3D数据集上展现出卓越表现，说明其在分子几何表征中的强大能力。该模型还在一个大型量子化学竞赛的数据集上获得领先成绩。进一步的实验表明，当模型仅用950个样本训练后，用其驱动MD17中的分子进行分子动力学模拟时，所得的原子间距离分布及势能面与从头算模拟高度一致，显示出数据效率与高保真度。为进一步评估其在真实应用中的价值，研究中使用了一个包含约一万种构象的166原子小蛋白Chignolin数据集，构象由复制交换分子动力学得到，并经DFT计算。在该数据集上的评估结果显示，ViSNet显著优于经验力场，且其模拟所得到的受力计算与DFT非常接近。此外，模型在几何表征与分子结构之间展现出合理的可解释性。

该方法的贡献可概括为：通过RGC模块以线性时间隐式提取多类高阶几何特征；通过向量–标量交互机制充分挖掘几何信息；在多个任务中取得领先的能量、力及量子性质预测结果；在小分子与大体系如Chignolin上实现高保真的分子动力学模拟；并在几何表征与分子结构之间提供了合理的解释能力。

2 结果

2.1 ViSNet概述

ViSNet是一种灵活的等变图神经网络，可根据原子坐标与原子序数预测分子的势能、原子受力以及多种量子化学性质。如图1a所示，模型由嵌入模块、多层堆叠的ViSNet模块以及输出模块组成。原子序数与原子坐标首先输入嵌入模块，随后经过ViSNet模块以提取并编码几何表征，最终由输出模块根据几何表征预测分子性质。需要注意的是，ViSNet属于能量守恒型势能模型，即其预测的原子受力来自势能对坐标的负梯度。

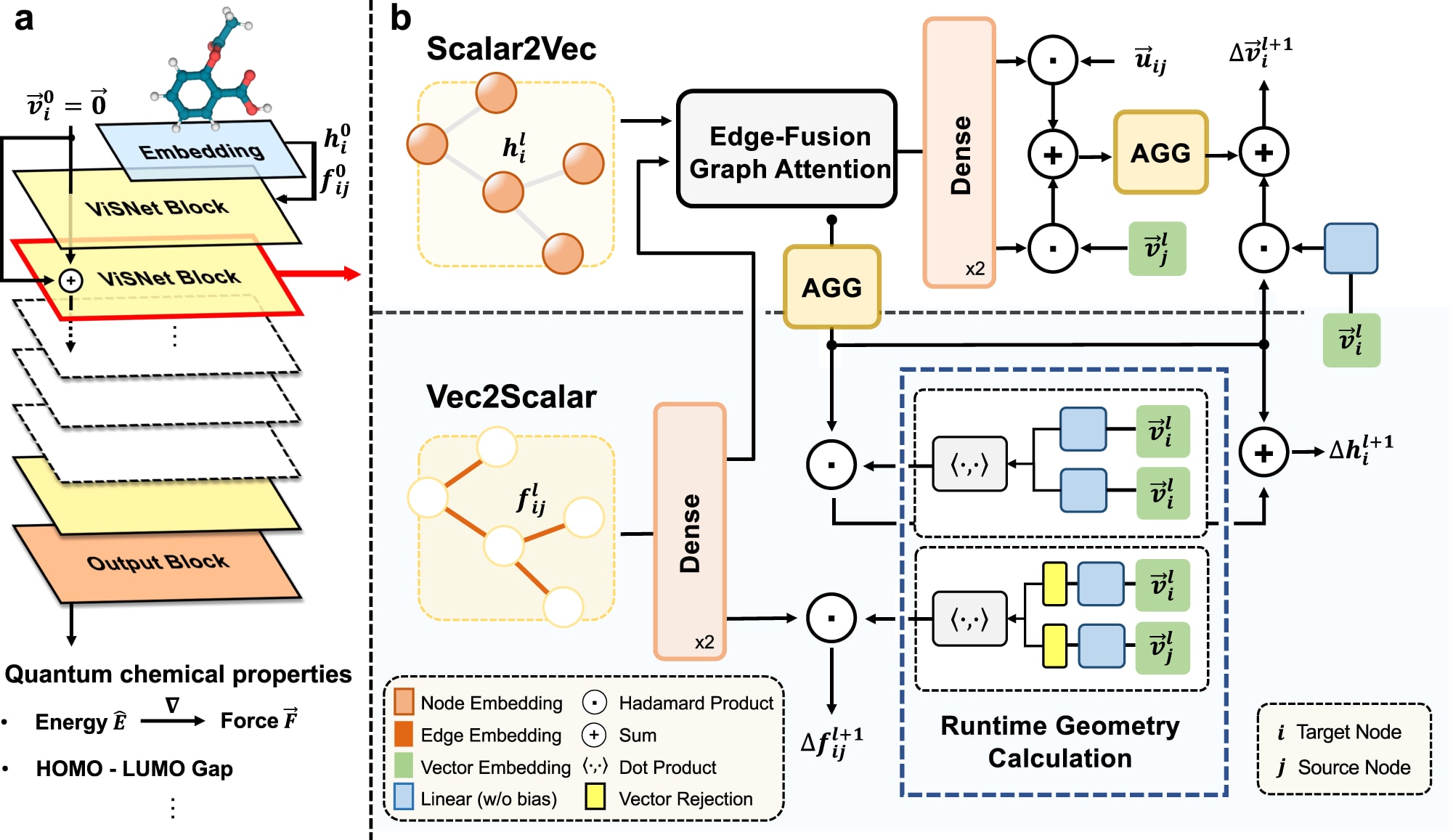
**图1 | ViSNet的整体架构a ViSNet的模型示意图。**ViSNet嵌入分子的三维结构，并通过一系列ViSNet模块提取几何信息，最终通过输出模块预测能量、力与HOMO–LUMO能隙等分子性质。b 单个ViSNet模块的流程图。一个ViSNet模块包含两个子模块：Scalar2Vec用于将标量嵌入附加到向量上；Vec2Scalar基于RGC策略更新标量嵌入。流程包括节点嵌入、边嵌入、方向单元、相对位置等输入，以及通过注意力与残差机制更新向量与标量嵌入。

经典力场的成功经验表明，诸如原子间距离、键角、二面角以及图2中的不正确扭转角等几何特征在决定分子总势能时具有重要作用。然而，以往研究对这些不变量几何特征的显式提取往往会在训练与推理过程中带来较高的时间或内存消耗。对于某一原子，其角度信息的计算复杂度随邻近原子数呈 $O (N^{2})$ 增长，而二面角的计算复杂度甚至达到 $O (N^{3})$ 。为缓解这一问题，受相关研究的启发，该研究提出运行时几何计算策略RGC，通过为每个节点引入等变向量表示（称为方向单元）来保存其几何信息。RGC直接利用方向单元计算几何特征，而方向单元仅需对目标节点至其所有邻居的向量求和一次，因此可将整体计算复杂度降至 $O (N)$ 。值得注意的是，除了采用PaiNN与ET中使用的角度信息外，ViSNet还利用更高阶的几何张量进一步计算二面角与不正确扭转角。

以图2所示由四个原子组成的示例结构为例，目标节点 $i$ 的角度信息可由向量 $r_{i j}$ 得到：

\begin{matrix} (1) & u_{i j} = \frac{{\vec{r}}_{i j}}{| {\vec{r}}_{i j} |}, {\vec{v}}_{i} = \sum_{j = 1}^{N_{i}} \vec{u_{i j}} \end{matrix}

方向单元 ${\vec{v}}_{i}$ 定义为从节点 $i$ 指向其所有邻居 $j$ 的单位向量之和。基于此，可得到方向单元的内积形式：

\begin{matrix} (2) & | {\vec{v}}_{i} |^{2} = \sum_{j = 1}^{N_{i}} \sum_{k = 1}^{N_{i}} ⟨ u_{i j}, u_{i k} ⟩ = \sum_{j = 1}^{N_{i}} \sum_{k = 1}^{N_{i}} \cos θ_{j i k} \end{matrix}

其中 $\vec{r_{i j}}$ 为节点 $i$ 指向邻居 $j$ 的向量， $\vec{u_{i j}}$ 为其单位向量。式(2)展示了方向单元内积表示的含义，即对由节点 $i$ 与任意两个邻居原子形成的角度 $θ_{j i k}$ 取余弦后求和。换言之，方向单元的内积包含了节点局部结构中的角度信息。

方向单元内积表示了从节点 $i$ 指向其所有邻居的单位向量之间的内积。结合式(1)，方向单元 ${\vec{v}}_{i}$ 的内积最终等同于节点 $i$ 与任意两个邻居原子所形成全部角度的余弦值之和。

与运行时角度计算类似，还可以计算节点 $i$ 的方向单元 ${\vec{v}}_{i}$ 以及节点 $j$ 的方向单元 ${\vec{v}}_{j}$ 在向量 $\vec{u i j}$ 与 $\vec{u_{j i}}$ 上的向量拒斥量。

向量拒斥量定义如下：

{\vec{w}}_{i j} = {Rej}_{\vec{u_{i j}}} ({\vec{v}}_{i}) = \vec{v} i - ⟨ \vec{v} i, \vec{u_{i j}} ⟩ \vec{u i j} = \sum_{m = 1}^{N_{i}} {Rej}_{\vec{u_{i j}}} (u_{i m})

\begin{matrix} (3) & {\vec{w}}_{j i} = {Rej}_{\vec{u_{j i}}} ({\vec{v}}_{j}) = {\vec{v}}_{j} - ⟨ {\vec{v}}_{j}, \vec{u_{j i}} ⟩ \vec{u_{j i}} = \sum_{m = 1}^{N_{j}} {Rej}_{\vec{u_{i j}}} (\vec{u_{j n}}) \end{matrix}

其中 ${Rej}_{\vec{b}} (\vec{a})$ 表示向量 $\vec{a}$ 在 $\vec{b}$ 方向上的正交分量，即向量拒斥。根据式(1)， $\vec{u_{i j}}$ 与 ${\vec{v}}_{i}$ 均已定义。 ${\vec{w}}_{i j}$ 表示所有单位向量的拒斥量之和 $R e j_{\vec{u_{j m}}} (\vec{u_{j m}})$ ，而 ${\vec{w}}_{j i}$ 则表示所有单位向量 $R e j_{\vec{u_{j n}}} (\vec{u_{j n}})$ 相对于 $u_{j i}$ 的拒斥量之和。接着，通过计算 ${\vec{w}}_{i j}$ 与 ${\vec{w}}_{j i}$ 的内积，可以得到边 $e_{i j}$ 对应的二面角信息：

\begin{matrix} (4) & ⟨ {\vec{w}}_{i j}, {\vec{w}}_{j i} ⟩ = \sum_{m = 1}^{N_{i}} \sum_{n = 1}^{N_{j}} ⟨ {Rej}_{u_{i j}} (u_{i m}), {Rej}_{u_{j i}} (u_{j n}) ⟩ = \sum_{m = 1}^{N_{i}} \sum_{n = 1}^{N_{j}} \cos φ_{m i j n} \end{matrix}

不正确扭转角来源于由四个节点形成的金字塔结构。在图2的示例中，节点 $i$ 位于金字塔顶部，不正确扭转角由两个共享边 $e_{i j}$ 的相邻平面构成。通过向量拒斥同样可以计算不正确扭转角：

{\vec{t}}_{i j} = {Rej}_{u_{i j}} ({\vec{v}}_{i}) = \sum_{m = 1}^{N_{i}} {Rej}_{u_{i j}} (u_{i m})

\begin{matrix} (5) & {\vec{t}}_{j i} = {Rej}_{u_{j i}} ({\vec{v}}_{i}) = \sum_{n = 1}^{N_{i}} {Rej}_{u_{j i}} (u_{i n}) \end{matrix}

类似地，两者内积代表边 $e_{i j}$ 所对应全部不正确扭转角余弦值的累积：

\begin{matrix} (6) & ⟨ {\vec{t}}_{i j}, {\vec{t}}_{j i} ⟩ = \sum_{m = 1}^{N_{i}} \sum_{n = 1}^{N_{i}} ⟨ {Rej}_{u_{i j}} (u_{i m}), {Rej}_{u_{j i}} (u_{i n}) ⟩ = \sum_{m = 1}^{N_{i}} \sum_{n = 1}^{N_{i}} \cos ψ_{m i j n} \end{matrix}

多项研究验证了高阶几何张量在分子建模中的有效性。然而，这些方法通常依赖Clebsch–Gordan积的计算，使得其计算成本过高，妨碍其在大体系中的应用。该研究在RGC思想基础上，将向量转换为球谐函数形式的高阶表示，同时以内积替代CG积。依据加法定理，扩展后的高阶张量仍可以以勒让德多项式的方式表示角度信息：

\begin{matrix} (7) & P_{l} (\cos θ_{j i k}) = P_{l} (⟨ u_{i j}, u_{i k} ⟩) \propto \sum_{m = - l}^{l} Y_{l, m} (u_{i j}) Y_{l, m}^{*} (u_{i k}) \end{matrix}

其中 $P_{l}$ 为 $l$ 阶勒让德多项式， $Y_{l, m}$ 为球谐函数， $Y_{l, m}^{*}$ 为其共轭。通过对不同阶 $l$ 的贡献进行求和，可以得到标量角度表示，这与使用内积的操作等价。此扩展不会增加模型规模，也不会改变其结构。此外，RGC的旋转不变性证明给出在后续附录中。

为充分利用几何信息并增强标量与向量之间的交互，设计了向量–标量交互式消息传递机制，用于分别在节点与边的交互中处理角度与二面角信息。与以往主要更新节点特征的研究不同，该方法在消息传递中同时更新节点与边特征，使几何表示更加完整。该机制的关键操作如下：

\begin{matrix} (8) & m_{i}^{l} = \sum_{j \in N (i)} ϕ_{m}^{s} (h_{i}^{l}, h_{j}^{l}, f_{i j}^{l}) \end{matrix}

\begin{matrix} (9) & {\vec{m}}_{i}^{l} = \sum_{j \in N (i)} ϕ_{m}^{v} (m_{i j}^{l}, {\vec{r}}_{i j}, {\vec{v}}_{j}^{l}) \end{matrix}

\begin{matrix} (10) & h_{i}^{l + 1} = ϕ_{u n}^{s} (h_{i}^{l}, m_{i}^{l}, ⟨ {\vec{v}}_{i}^{l}, {\vec{v}}_{i}^{l} ⟩) \end{matrix}

\begin{matrix} (11) & f_{i j}^{l + 1} = ϕ_{u e}^{s} (f_{i j}^{l}, ⟨ {Rej}_{{\vec{r}}_{i j}} ({\vec{v}}_{i}^{l}), {Rej}_{{\vec{r}}_{j i}} ({\vec{v}}_{j}^{l}) ⟩) \end{matrix}

\begin{matrix} (12) & {\vec{v}}_{i}^{l + 1} = ϕ_{u n}^{v} ({\vec{v}}_{i}^{l}, m_{i}^{l}, {\vec{m}}_{i}^{l}) \end{matrix}

其中 $h_{i}$ 表示节点 $i$ 的标量嵌入， $f_{i j}$ 为节点对 $(i, j)$ 的边特征， ${\vec{v}}_{i}$ 为RGC中的方向单元嵌入，变量上标 $l$ 表示其所在的网络层。为简洁起见，不正确扭转角项未在此列出，其更完整描述见补充材料。ViS-MP扩展了传统消息传递、聚合与更新过程，使向量与标量嵌入之间能够充分交互。式(8)与式(9)分别对应标量消息与向量消息的计算与聚合。式(10)与式(11)展示了节点与边的更新方式，其中节点嵌入受聚合标量消息与方向单元内积影响，边嵌入则通过方向单元拒斥量的内积进行更新。最后，向量嵌入在式(12)中根据标量与向量消息共同更新。向量更新函数需保持等变性，其详细形式及等变性证明见方法部分与补充材料。

总而言之，RGC策略通过内积提取几何特征，而在ViS-MP中，标量嵌入与向量嵌入彼此循环更新，使模型能够从分子结构中学习到更为完整的几何表征。

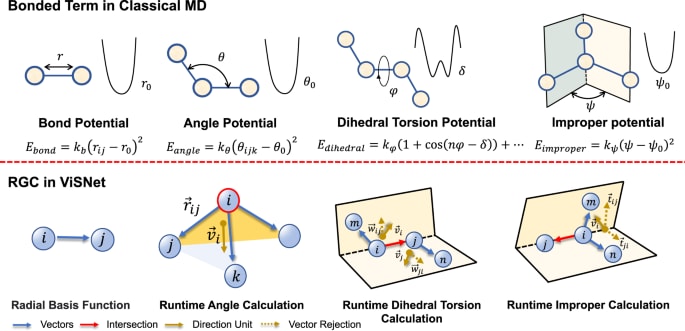
**图2 | 运行时几何计算（RGC）模块示意及其与经典分子动力学键合项的关系键合项包括键长、键角、二面角与不正确扭转角。**RGC模块以线性时间复杂度表示经典分子动力学的所有键合项。黄色箭头表示方向单元 $v_{i}$ 。

2.2 精确的量子化学性质预测

为了评估ViSNet在量子化学性质预测中的表现，模型在多个主流基准数据集上进行了测试，包括MD17、修订版MD17、MD22、QM9、Molecule3D以及OGB-LSC PCQM4Mv2，这些任务涉及能量、力以及其他分子性质的预测。MD17包含七种小型有机分子的分子动力学轨迹，每种分子拥有从数十万到近百万不等的构象数。修订版MD17在数值精度上更为可靠。MD22是近年提出的更大规模的分子动力学数据集，其分子大小显著增加，范围从42个原子到370个原子，涵盖蛋白、脂质、碳水化合物、核酸以及超分子等复杂体系。QM9包含133385个小型有机分子，提供12类量子化学性质。Molecule3D则包含3899647个来自PubChemQC的数据，其基态结构与性质均基于DFT计算。ViSNet在此任务中侧重预测HOMO-LUMO能隙。PCQM4Mv2源自大型量子化学数据库，包含数百万分子的DFT计算HOMO-LUMO能隙，训练集中提供部分分子的三维结构，而验证与测试集不提供三维信息。

在这些任务中，ViSNet与多种先进方法进行了对比，包括DimeNet、PaiNN、SpookyNet、ET、GemNet、UNiTE、NequIP、SO3KRATES、Allegro、MACE等。结果显示，无论是小分子（MD17与修订版MD17）还是大分子体系（MD22），ViSNet在能量与力的预测上均取得最低的平均绝对误差。相较于采用较低几何阶数或未充分利用几何交互的模型，ViSNet通过强化几何特征的提取与交互获得性能提升；而相较于依赖高阶群表示且计算成本较高的模型，ViSNet通过球谐函数与内积替代Clebsch–Gordan积也展现出高效且准确的特性。

在QM9数据集上，ViSNet在12类量子化学性质中，有9项取得最佳表现，其他性质也达到了接近领先的结果。在Molecule3D的测试中，ViSNet在随机划分与骨架划分下均表现显著优于现有方法，尤其在随机划分中取得大幅性能优势。此外，ViSNet具有良好的可迁移性，可与其他多模态方法结合，例如Transformer-M，并在PCQM4Mv2数据集上取得突出成绩，成功获得NeurIPS 2022大赛PCQM4Mv2赛道的第一名。

为了进一步评估计算效率，ViSNet的推理时间也与多种模型进行了比较。延迟被定义为在一组给定坐标上计算力（即梯度）所需的时间。结果显示，在相同网络深度下，ViSNet显著快于部分高阶张量模型。例如，ViSNet在两层结构下比MACE节省约42.8%的时间；虽然Allegro通过高效的CG积实现了加速，但ViSNet在不同深度下仍保持更低的延迟，显示其在精度与效率上的平衡优势。

表1｜MD17数据集中7种小型有机分子的能量（kcal/mol）与受力（kcal/mol/Å）平均绝对误差，与先进算法的对比

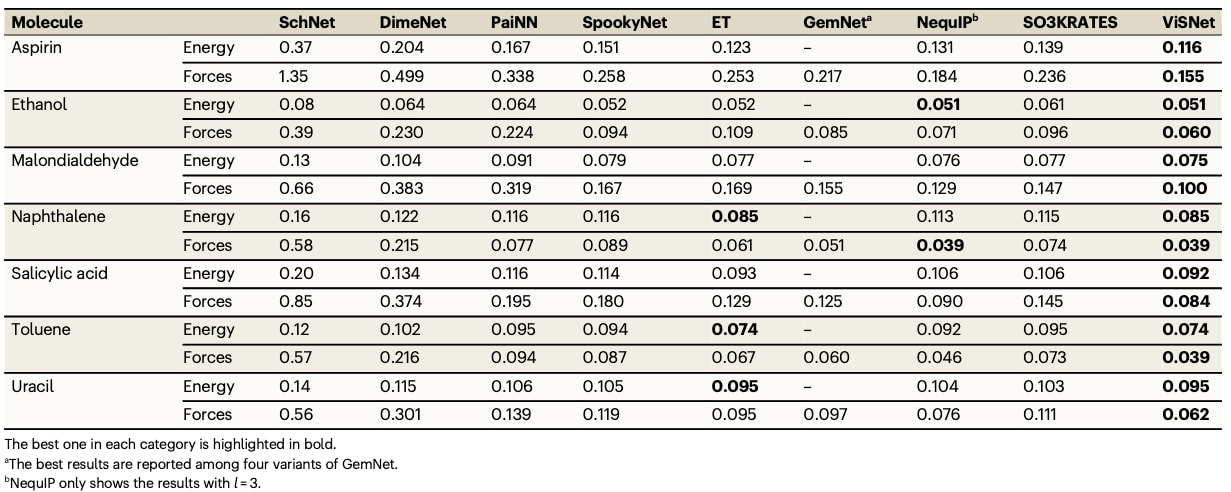
表2｜rMD17数据集中10种小型有机分子的能量（kcal/mol）与受力（kcal/mol/Å）平均绝对误差，与先进算法的对比

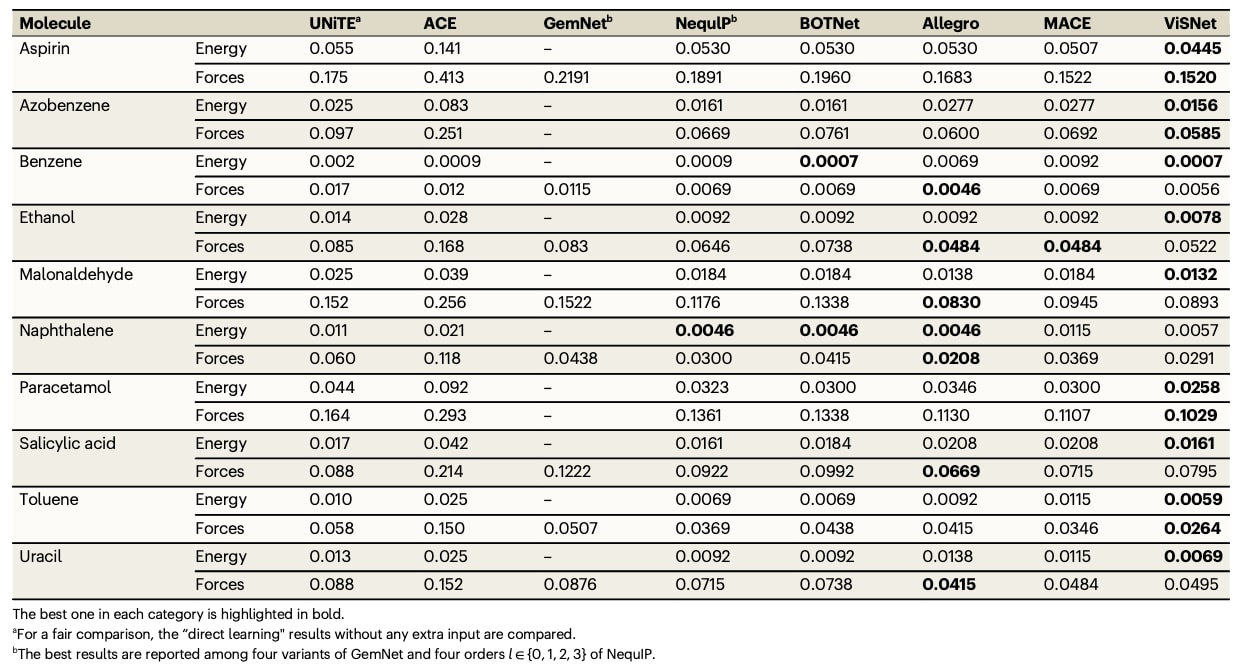
表3｜MD22数据集中7种大规模分子的能量（kcal/mol）与受力（kcal/mol/Å）平均绝对误差

表4｜QM9数据集中12类分子性质的平均绝对误差，与先进算法的对比

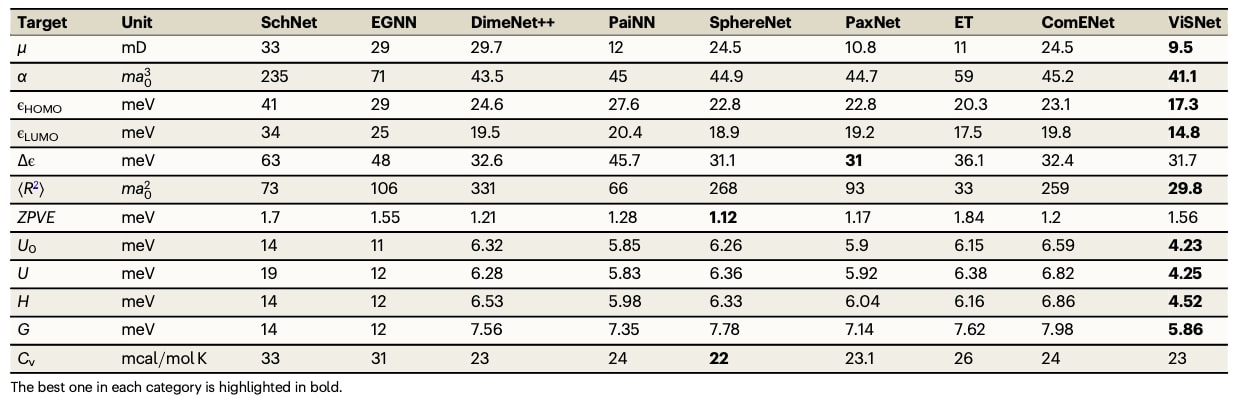
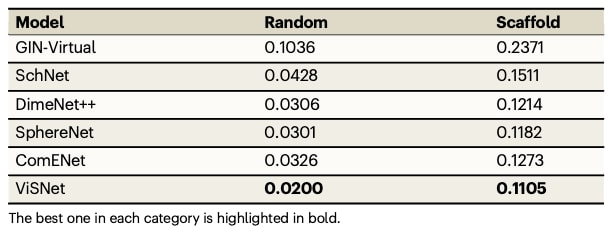
表5｜Molecule3D测试集中HOMO–LUMO能隙（eV）在随机划分与骨架划分下的平均绝对误差，与先进算法的对比

2.3 高效的分子动力学模拟

为了评估ViSNet在分子动力学模拟中的潜力，该研究将仅使用950个样本训练得到的ViSNet模型引入ASE模拟框架，对MD17数据集中全部七种有机分子执行分子动力学模拟。模拟时间步长设为 $τ = 0.5 fs$ ，温控方式采用Berendsen恒温器，其余设置与MD17数据集保持一致。通过计算ViSNet驱动模拟所得的原子间距离分布，并与DFT级别的从头算分子动力学结果进行对比，可以观察到两者的分布高度一致。原子间距离分布 $h (r)$ 定义为以某一原子为中心、半径为 $r$ 处的平均原子密度。对七种分子的分析显示，ViSNet与DFT在所有分子上均给出了相近的构象分布。此外，还比较了两者对势能面的采样结果，结果显示势能面同样具有高度一致性。这些现象均表明ViSNet在探索构象空间方面具有较高保真度，即使训练样本量极其有限仍能取得与量子模拟接近的效果。

相较于DFT，已有多项基于机器学习的力场方法，如sGDML、ANI、DPMD与PhysNet，已展示出在分子动力学模拟中显著的加速优势。ViSNet同样具备这一特性，其计算成本相对于DFT也大幅降低，相关结果可由补充材料中的数据与图表进一步说明。

为了进一步检验ViSNet在分子动力学性质方面的表现，在MD17数据集中以乙醇为对象进行了500 ps的NVE系综模拟，时间步长为 $τ = 0.5 fs$ ；在MD22数据集中以Ac-Ala3-NHMe为对象进行了200 ps的模拟，时间步长为 $τ = 1 fs$ 。模拟分别由ViSNet、sGDML以及DFT驱动。对于乙醇，分析了其振动光谱以及羟基二面角的概率分布。三种方法均给出了相似的振动光谱，仅在峰强度上存在少量差异。羟基二面角的分布呈现出三个主要构象：gauche±与trans，与已知的乙醇构象一致。

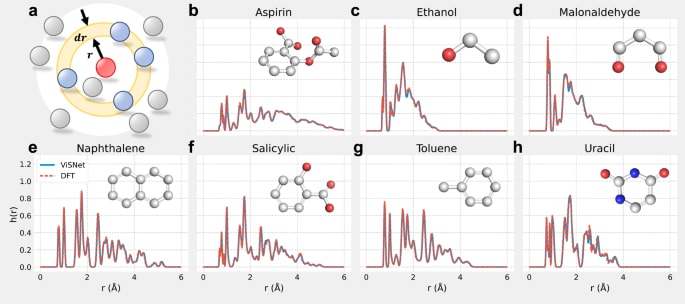
对于Ac-Ala3-NHMe，则通过Ramachandran图比较了三种方法的采样能力。自由能景观通过平均力势估计， $ϕ$ 与 $ψ$ 作为反应坐标，并将所有二面角分为40×40的网格进行统计。不同方法所得的能量景观整体保持一致。尽管ViSNet在MD22训练任务中的预测精度优于sGDML，但在如此小规模的肽段体系中，由于本身构象空间有限，两者在动态采样能力上的差异并不显著，因此在Ramachandran图中的表现也非常接近。这一现象说明在仅使用少量训练样本时，ViSNet仍能够维持高质量的分子动力学行为，并展现出与量子计算相符的可靠性与效率。

图 3｜由ViSNet与DFT驱动的分子动力学模拟中原子间距离分布 a 示意图展示以任意原子为中心、半径为 $r$ 处的原子密度。原子间距离分布被定义为原子密度的系综平均。b–h 展示MD17中全部七种有机分子的原子间距离分布，由ViSNet驱动的模拟结果以蓝色实线表示，DFT结果以橙色虚线表示。对应分子的结构示意图显示在右上角。源数据在附带的Source Data文件中提供。

2.4 全原子蛋白体系中的应用

为了检验ViSNet在真实场景中的适用性，研究中选用了包含166个原子的迷你蛋白Chignolin（如图4a所示）。该蛋白的数据集由复制交换分子动力学采样而来，包含约10000种不同构象，并通过DFT计算得到对应能量与受力信息。数据集按照8:1:1的比例划分为训练集、验证集与测试集。在这一数据集上，ViSNet与多种先进的机器学习力场进行了比较，包括ET、PaiNN、GemNet-OC、MACE、NequIP与Allegro，同时也与经验力场进行了比较，DFT结果作为基准。

图4b展示了Chignolin的自由能景观，以D3主链羰基氧与G7主链氮之间的距离 $d_{D 3 - G 7}$ 以及E5主链羰基氧与T8主链氮之间的距离 $d_{E 5 - T 8}$ 作为坐标。左侧较为集中的区域对应折叠态，右侧较分散的区域对应未折叠态。从这些区域中随机选取六种构象进行可视化，其中四种构象的预测误差小于模型在该数据集上的平均绝对误差，其余两种则大于该误差。值得注意的是，在所有模型中，高能量（对应采样概率低）的构象均表现出较高误差，而低能量区域的构象预测更为准确。这一现象说明，高能量构象的采样不足会限制模型在该区域的泛化能力。

补充材料中的图S6展示了所有机器学习力场与经验力场在测试集上的预测能量与DFT能量的相关性。ViSNet取得更低的平均绝对误差与更高的 $R^{2}$ 值。图S7中的小提琴图进一步显示，ViSNet、PaiNN与ET的误差分布显著优于其他模型，而经验力场的误差分布范围更大。原子力的相关性分析也表现出类似趋势，具体展示在图S8中。

为了更全面地比较模型性能，还将模型的预测精度、训练耗时与模型规模结合进行分析，如图5所示。尽管ViSNet在训练速度上略慢于ET与PaiNN，但其通过引入更丰富的几何信息获得了更高的预测能力。与同样计算二面角的GemNet相比，ViSNet的运行时几何计算将显式二面角计算的复杂度从 $O (N^{3})$ 降低至 $O (N)$ ，使其在计算成本上更具优势。同时，相较于采用Clebsch–Gordan积的MACE、Allegro与NequIP等模型，ViSNet在模型规模与训练速度上也保持更高效率。

在此基础上，还对Chignolin进行了分子动力学模拟。随机选取10种构象作为初始结构，对每一种构象运行100 ps的模拟。图4c展示了10条轨迹在模拟过程中相对于起始构象的平均RMSD，并以阴影表示标准差范围。图4d展示了模拟过程中由ViSNet计算的原子力与DFT力之间的逐分量平均绝对误差，并同样以阴影表示标准差范围。模拟结果显示，三维力的三个分量均保持较低误差，未出现偏向性。整体上，ViSNet驱动的分子动力学轨迹与量子化学计算之间高度一致，说明其在真实体系中的潜在应用价值。

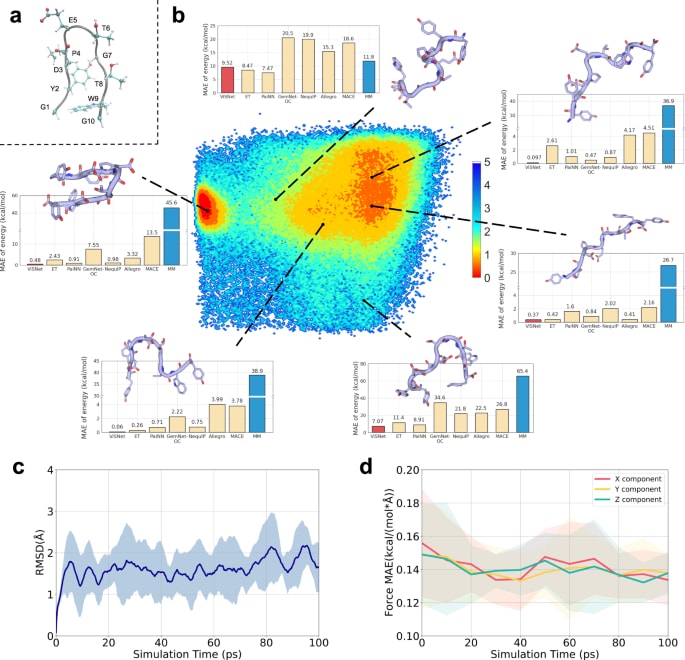
图 4｜ViSNet在Chignolin构象空间评估与分子动力学模拟中的应用。 a Chignolin结构的可视化。主链以灰色表示，各残基的侧链以球棍形式突出显示。b 通过REMD采样得到的Chignolin能量景观。能量景观的x轴为D3主链羰基氧与G7主链氮之间的距离，y轴为E5主链羰基氧与T8主链氮之间的距离。随后选取六种构象进行可视化，每个构象以卡通形式呈现，残基以棍状表示。直方图展示了在这些构象上，各类机器学习力场（包括ViSNet、ET、PaiNN、GemNet-OC、NequIP、Allegro与MACE）以及分子力学计算的能量差与DFT基准的绝对误差。c 由ViSNet驱动模拟的10条Chignolin轨迹，其平均均方根偏差（RMSD）。阴影区域表示标准差范围。d 模拟过程中原子力各分量的平均绝对误差（MAE），模拟由ViSNet驱动。基准能量与受力由Gaussian 16计算得到。阴影区域表示标准差范围。源数据在附带的Source Data文件中提供。

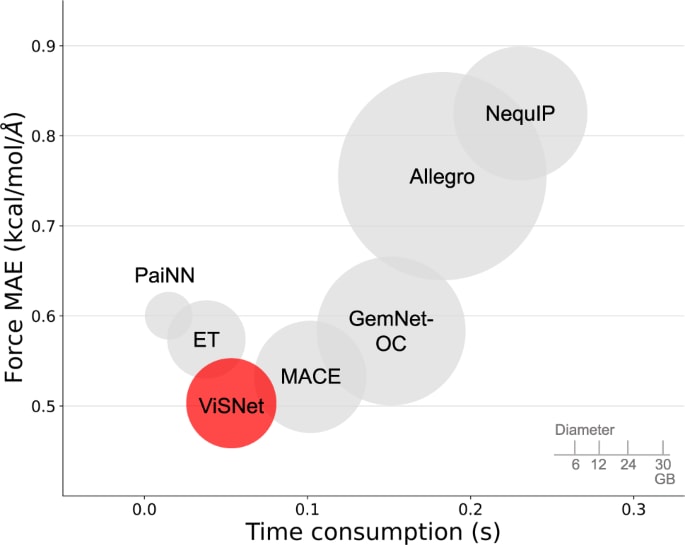
图 5｜在Chignolin任务中，ViSNet（红色）与其他算法（灰色）在模型性能（纵轴）、训练时间消耗（横轴）以及训练内存消耗（体积）上的比较在这一比较中所包含的算法包括PaiNN、ET、MACE、GemNet-OC、Allegro与NequIP。PaiNN与ET的训练速度更快、模型规模更小，这是因为ViSNet进一步纳入了二面角计算。得益于运行时几何计算，ViSNet相较GemNet-OC表现更优，将显式二面角提取的复杂度从 $O (N^{3})$ 降低到 $O (N)$ 。此外，由于简化了CG积相关运算，ViSNet在速度与规模上也优于MACE、Allegro与NequIP。ViSNet之所以获得最佳性能，源于其精心设计的运行时几何计算以及向量–标量交互式消息传递机制。源数据在附带的Source Data文件中提供。

2.5 ViSNet在分子结构上的可解释性

为了展示ViSNet捕获几何信息的能力，对其在分子结构上的可解释性进行了分析。该分析基于MD17数据集中的七种分子以及MD22中的两个分子体系，以验证ViSNet是否能够从分子结构中学习到与化学直觉一致的几何表征。

分析首先通过计算模型预测能量对原子坐标的梯度，得到原子级的敏感性评分。对MD17数据集中的七种小分子进行敏感性分析后可以观察到，敏感性评分与分子中典型的结构特征呈现高度一致性。例如，在甲醛与甲醇等分子中，碳氧双键以及羟基等具有强相互作用的化学键在敏感性图中表现为更高的梯度强度，这说明模型在能量预测中高度依赖这些关键的局部结构特征。更重要的是，ViSNet中的方向单元向量 ${\vec{v}}_{i}$ 可用于进一步揭示其内部对几何信息的利用。通过将方向单元映射回三维空间，可以看到其方向分布通常与化学键方向或相邻原子的空间排布保持一致，从而表明向量嵌入中确实编码了与分子局部几何对应的信息。

在MD22中的较大体系Ac-Ala3-NHMe和Uracil-Water中，类似的分析同样显示出模型对关键几何结构的敏感性。例如，在肽段体系中，与肽键扭转相关的二面角区域在模型的敏感性图中具有更高的响应；在Uracil-Water体系中，涉及氢键相互作用的结构单元因其在体系能量中占据核心地位，也表现出更高的敏感性。这些现象说明，ViSNet不仅能够有效捕获局部结构中的简单角度与距离特征，也能够识别更复杂的高阶几何关系。

为了更加系统地解释ViSNet对几何表征的学习方式，还将方向单元的内积、向量拒斥量以及高阶张量扩展的标量输出与传统化学几何量进行对比。结果表明，这些内部量与真实的角度分布、二面角分布以及不正确扭转角分布之间均具有明显相关性，如在数据集中不同温度与构象区域中均能看到一致的趋势。由此可见，ViSNet通过RGC与向量–标量交互机制，确实在内部构建了与传统分子力场中使用的几何特征近似一致的表征结构。

总体而言，ViSNet在学习分子几何表征方面展现出较高的可解释性，使其在能量预测与分子动力学模拟任务中不仅具有精度优势，也具备良好的透明度与可信度。

3 总结

该研究提出了ViSNet，这是一种用于分子动力学模拟的几何深度学习势能模型。基于群表示理论的方法与基于方向信息的方法是实现SE(3)等变性的两类主要几何深度学习势能模型。ViSNet在设计中融合了两者的优势，通过RGC策略与ViS-MP机制实现高效且充分的几何信息利用。一方面，RGC策略能够以轻量级计算方式显式提取并利用方向几何信息，使模型训练与推理更为迅速；另一方面，ViS-MP包含一系列高效的向量–标量交互操作，能够更充分地发挥几何信息的作用。

此外，根据多体展开理论，一个体系的总势能可视为每个原子的单体势能与从两体到多体的能量修正项之和。以往研究通常通过堆叠 $k$ 层消息传递模块，以 $k$ 跳邻域层级地模拟截断的能量修正项。与此不同，ViSNet在单个模块中就编码了角度、二面角以及不正确扭转角信息，使其具备更强的表征能力。

ViSNet的普适性或完备性目前尚未通过几何Weisfeiler–Leman测试验证，这是由于模型采用了内积操作，该操作具有计算效率，但无法区分某些具有相同角度信息的原子反射结构。若要通过相关反例或通过GWL测试，未来模型需在更高阶球谐函数的基础上引入Clebsch–Gordan积。

除了在能量、力以及化学性质上实现高精度预测外，以接近从头算精度执行分子动力学模拟，同时保持经验力场级别的计算成本，也是一个重要挑战。ViSNet在真实场景的从头算分子动力学模拟中表现出可行性，并能扩展至蛋白等大型分子体系。未来的研究方向将致力于进一步拓展ViSNet以支持更大规模且更复杂的分子体系。