WIREs Comput. Mol. Sci. 2024 | 扩散模型在蛋白质和对接中的应用

这篇综述《Diffusion Models in Protein Structure and Docking》系统总结了扩散模型在蛋白质结构预测与设计中的前沿应用，内容图文并茂、结构清晰，非常适合作为入门教材与研究参考。

文章围绕扩散模型的基本原理、几何建模方法与结构生物学中的具体实践展开，重点涵盖了蛋白质主链的无条件与条件生成、小分子对接、蛋白–配体相互作用等任务。特别是对于如何在欧几里得空间与流形上建模，以及如何实现 SE(3) 等变性等关键问题，做了深入而易懂的讲解。

此外，文中还对评估指标、自洽性分析、构象建模策略等核心议题提供了系统梳理，是扩散模型开发者与结构生物学从业者的极佳参考资料。

Yim, Jason, Hannes Stärk, Gabriele Corso, Bowen Jing, Regina Barzilay, and Tommi S. Jaakkola. “Diffusion Models in Protein Structure and Docking.” WIREs Computational Molecular Science 14, no. 2 (2024): e1711. https://doi.org/10.1002/wcms.1711.

0 | 摘要

随着生成式人工智能的迅猛发展，计算结构生物学的研究前沿正经历深刻变革。特别是在蛋白质设计和药物发现领域，近来的突破性成果极大推动了进展。而在这些成果背后，扩散模型（Diffusion Models, DM）正扮演着核心角色。扩散模型最初起源于计算机视觉领域，并迅速在图像生成任务中占据主导地位，展现出卓越的生成质量与性能。随后，该类模型被拓展并改造以适用于其他领域，其中就包括计算结构生物学。扩散模型擅长处理高维几何数据，并充分发挥深度学习的关键优势。在结构生物学中，扩散模型已经在蛋白质三维结构生成与小分子对接（docking）等任务中取得了最先进（state-of-the-art）的成果。本综述介绍了扩散模型的基本原理、与分子表示相关的建模选择、生成能力、主流启发式策略、以及其存在的关键局限与未来改进方向。同时也提供了评估流程中的最佳实践建议，以推动建立更加严格的基准体系与评价方法。这篇综述不仅系统梳理了该领域的最新进展，也强调了当前生成技术在计算结构生物学中的潜力与挑战。

1 | 引言

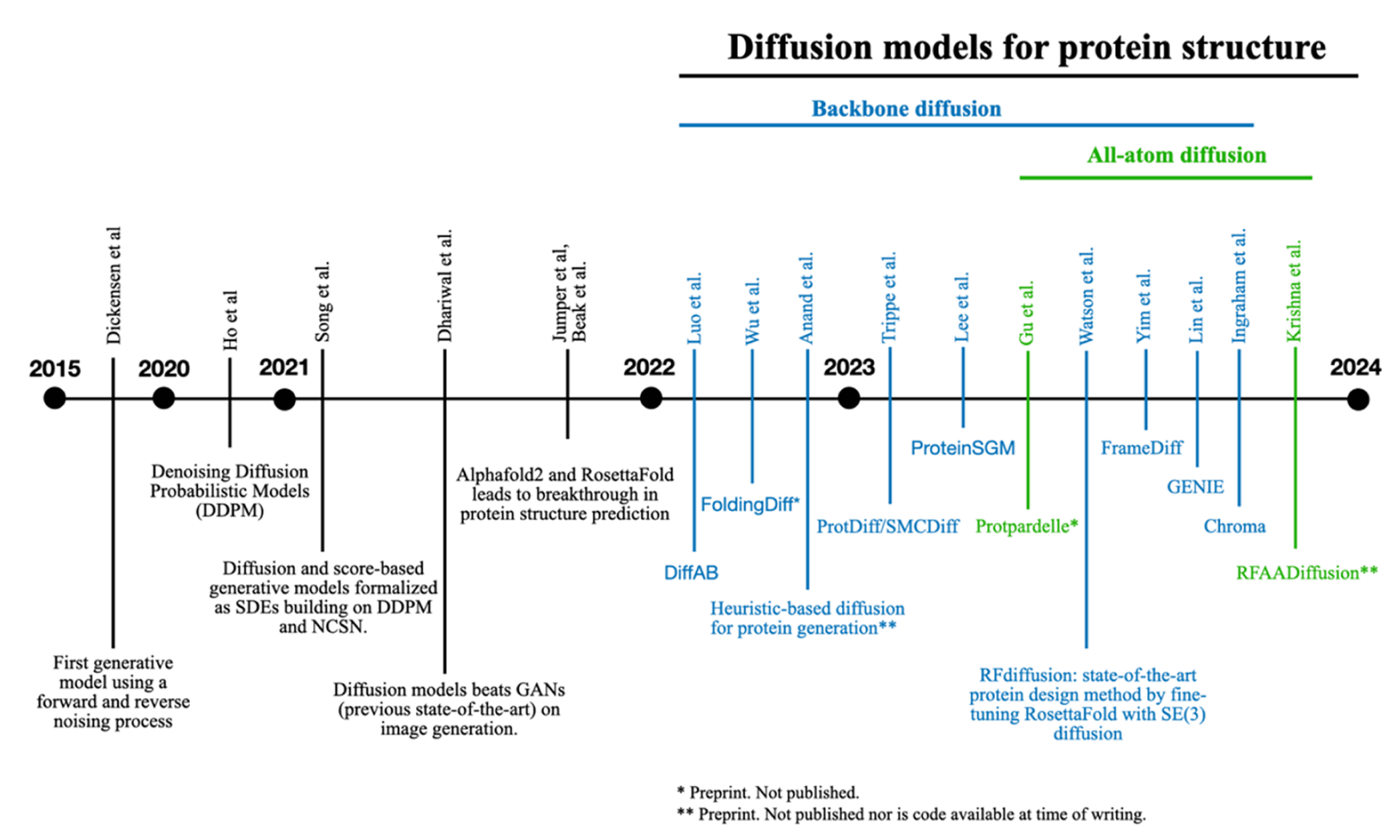
图 1 | 扩散模型的发展时间线，从其最初提出到在结构生物学中用于蛋白质建模的过程。2021 年，AlphaFold2 的问世与图像生成领域中扩散模型的发展，为其在结构生物学中的应用奠定了基础。当时，研究者借助 AlphaFold2 中的神经网络架构、蛋白质表示方法以及建模技术，推动扩散模型首次进入蛋白质结构建模领域。从 2022 年至今，蛋白质结构专用扩散模型的研究进入快速发展阶段。早期方法主要聚焦于主链扩散建模（backbone diffusion），而现今已有越来越多的工作开始探索全原子建模（all-atomic systems），推动蛋白质建模迈向更高的精度与生物物理真实感。

蛋白质的结构建模与理解是推动生物知识获取、新药研发以及生物技术创新的核心动力。然而，计算结构生物学长期受到实验数据稀缺的限制，这主要源于解析单个蛋白质结构所需的高昂成本、时间与人力投入。尽管如此，PDB 等数据库中积累了数十年的结构数据，并伴随着近年来实验技术的快速发展，使得计算建模迎来了一个关键转折点。

深度学习在结构生物学中的第一次重大突破来自 AlphaFold2（AF2），它在 CASP 14 比赛中首次实现了从氨基酸序列预测蛋白质三维结构的原子级精度，彻底革新了蛋白结构解析的问题。

尽管如此，AF2 及其相关方法的一个根本性局限在于：它们无法基于生物物理属性生成结构分布。例如，在药物发现场景中，需要模型既能在配体存在的条件下建模蛋白结构，又能对不同温度下的构象进行采样，以刻画结构异质性对功能的影响。而在生物分子设计中，模型往往被要求生成全新的分子，这些分子本质上属于训练分布之外，用于发现新型结合物与酶。

要解决这些问题，必须转向生成式模型（generative models）。相比传统方法，生成模型具备灵活的概率建模能力，能够直接在给定条件下进行采样和生成。早期的生成模型，如变分自编码器（VAE），由于难以编码天然的几何约束，表现不佳；**生成对抗网络（GAN）**则因训练与优化困难，也未能奏效。**连续归一化流（CNFs）**在考虑对称性的基础上相较 VAE 有所改进，但在高维数据上无法扩展。

如今，一类全新的生成模型——扩散模型（Diffusion Models, DM），继承了 CNF 的优势，并通过可扩展的训练方式成功在高维数据上建立深度神经网络。这些模型最初在计算机视觉中取得突破，随后迅速在结构生物学中成为最前沿的技术手段。

几何深度学习、生成模型与结构生物学的交叉融合使得扩散模型已经在以下任务中超越了传统方法：

全新蛋白质设计（de novo protein design）
小分子生成设计（small molecule design）
分子构象生成（molecular conformer generation）
盲对接任务（blind protein–ligand docking）

使用生成式人工智能的另一个显著优势在于：能够快速整合大规模数据集以指导实验设计。如今，扩散模型正在赋能生成式 AI，加速计算结构生物学的研究与应用进程。

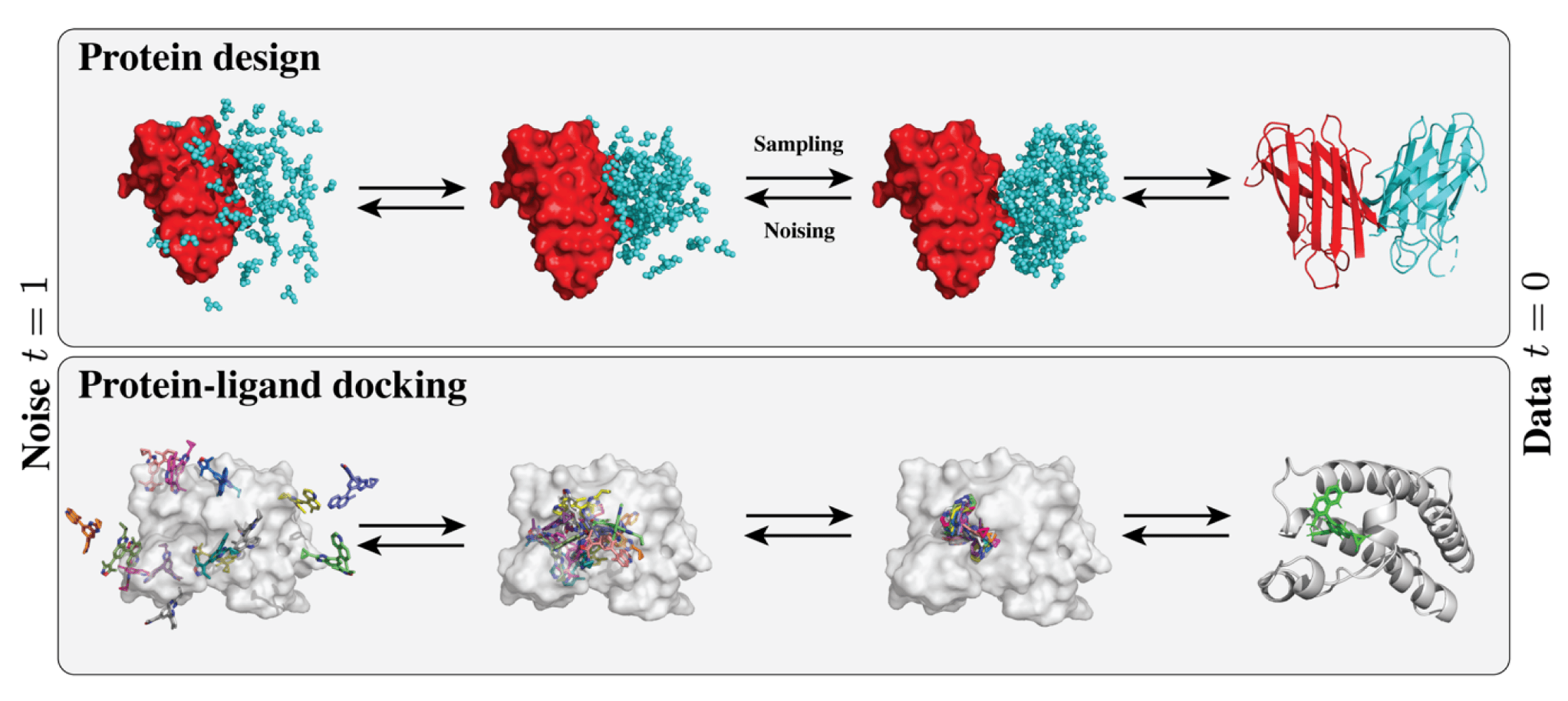
本综述总结了扩散模型（Diffusion Models, DMs）在结构生物学领域的最新进展。尽管结构生物学应用广泛，本文聚焦于两个关键子方向：蛋白质结构的生成式应用与蛋白–配体对接（docking），如图 2 所示。

在每个子方向中，本文进一步围绕以下几个核心议题展开讨论：

(i) 三维分子数据的多种表示方式选择
(ii) 具体的建模任务
(iii) 每种方法中的启发式假设
(iv) 评估方法中的最佳实践

尽管评估相关问题并非扩散模型特有，但在生成模型日益普及的当下，评估标准的讨论尤为重要。

该综述的结构如下：

首先，研究者们提供扩散模型的技术背景与理论综述，包括其在欧几里得空间中的原始形式，以及如何将其推广到满足几何对称性的流形空间上——这两者在处理分子三维数据时都极为常见。

接下来，研究者们回顾了扩散模型在蛋白质结构生成上的应用，涵盖：

(i) 无条件生成（unconditional regime）：目标是生成全新、丰富且高质量的蛋白质；
(ii) 蛋白设计（protein design）：生成具备特定性质的蛋白质。

第二个重点应用是蛋白–配体对接（protein–ligand docking）。对接任务中，处理配体与蛋白质的柔性结构是一大挑战，本文也详细讨论了现有的建模方法。研究者们特别强调了在上述任务中已取得最先进性能的扩散模型方法，并在最后对该领域的发展方向与当前存在的局限性进行了总结。综上所述，该综述旨在通过解析最新技术背后的原理，系统梳理扩散模型在蛋白质结构生成与对接中的迅速进展，为理解并参与该领域的前沿研究提供参考与启发。

图 2 | 展示了扩散模型在结构生物学中的应用场景，这些方向已达到当前的最先进水平。图中展示了扩散过程包含的两个方向：前向（加噪）与反向（采样）。扩散从 t = 1 开始，此时为易于采样的噪声分布，模型通过引导该过程逐步趋近于真实数据分布，在 t = 0 时生成结构数据。蛋白质设计任务中，扩散模型在生成蛋白质时可基于一个或多个条件进行控制，例如要求其能够与另一蛋白结合，如图中所示。蛋白–配体对接任务中，模型生成多个配体，并寻找在目标蛋白上的最佳结合构象，这是药物虚拟筛选中的关键步骤。

2 | 用于结构生物学的扩散模型

扩散模型（Diffusion Models, DM）是一类概率生成模型，其生成过程是通过逐步将噪声样本“净化”为真实数据来实现的。该模型的学习依赖于所谓的前向（扩散）过程，该过程则执行相反的操作：通过逐步添加噪声将原始数据扰动，最终将其转化为接近纯噪声的状态。随后，训练一个深度神经网络来反向还原这个过程，即从噪声逐步恢复至真实数据。

从更抽象的角度来看，扩散模型的目标是学习在两个分布之间进行插值：一个是容易采样的简单噪声分布（通常为高斯分布），另一个是真实的数据分布。神经网络进而拥有了将噪声样本逐步变换为结构数据的能力。

扩散模型的灵感最早可追溯至非平衡统计物理，其中Fokker–Planck 方程描述了在加性噪声存在下，初始概率分布随时间演化的过程。后续研究不断优化了训练与推理技术，最终使得扩散模型在计算机视觉领域取得了最先进的性能表现。

关于扩散模型的通用发展与技术综述，可参考 Yang 等人所作的详细综述文献。迄今为止，大多数扩散建模技术集中在图像与文本领域。

然而，在结构生物学的语境下，尤其是涉及蛋白质结构与对接任务时，理解扩散模型还需补充特定背景知识。本文后续将从两个方面展开：

欧几里得空间中的扩散模型的背景与关键技术细节
与图像和文本不同，蛋白质与分子数据涉及几何对称性与流形（manifold）上的建模问题，这将在后文中进一步介绍

2.1 | 欧几里得空间中的扩散模型

扩散模型（DM）中的前向与反向（生成）过程均可通过**随机微分方程（Stochastic Differential Equations, SDE）**进行建模。前向过程从数据分布 $x_{0} \sim p_{0}$ 开始，通过连续的加噪操作将 $x_{0}$ 转化为噪声 $x_{τ} \sim p_{τ}$ ，其中 $p_{τ}$ 是一个简单的先验分布，通常为高斯分布。无损失地可将 $τ = 1$ 设为前向扩散过程的终点时间。那么从数据到噪声的演化过程 $t \in [0, 1]$ 可由以下 SDE 描述：

\begin{matrix} (1) & d x = f (x, t) d t + g (t) d B \end{matrix}

直观来看，该方程描述了 $x$ 如何随着时间被连续扰动为噪声。在 SDE 中，扰动来自扩散项 $g (t) d B$ ，其中 $g (t)$ 通常是一个与时间相关的标量（扩散系数）， $d B$ 表示 $d$ 维布朗运动，对应于均值为 0、方差为 $d t$ 的高斯扰动。若 $g (t) = 0$ ，则上式变为普通微分方程（ODE），此时前向与反向过程均为确定性路径。

漂移项 $f (x, t) d t$ 则表示在无噪声情况下 $x$ 的确定性轨迹。在前向过程中， $f (x, t)$ 的作用是腐蚀数据，使得在 $t = 1$ 时 $x_{1}$ 完全变为噪声。图 3 可视化展示了漂移与扩散的共同作用。

在固定时间 $t$ 下，可以尝试建模分布 $p_{t} (x)$ ，即前向过程在时间 $t$ 下的状态分布。精确求解 $p_{t} (x)$ 通常需要对式 (1) 的Fokker–Planck 方程进行求解，但这依赖于具体的 $f (x, t)$ 与 $g (t)$ 的形式，通常难以获得解析解。后文将介绍一种方法，使得建模中并不需要显式求出 $p_{t} (x)$ 。

Anderson 等人的开创性工作指出，式 (1) 可通过另一条 SDE 反向重建，即从噪声开始，重构所有时间点上的 $p_{t} (x)$ ，尤其是 $t = 0$ 时的数据分布。该反向 SDE如下：

\begin{matrix} (2) & d x = [f (x, t) - g (t)^{2} \nabla \log p_{t} (x)] d t + g (t) d B \end{matrix}

在统计学中， $\nabla \log p_{t} (x)$ 被称为Stein Score，它引导 $x$ 向更高概率密度的区域演化。这一术语也广泛用于扩散模型中，故本文沿用之。由于 $p_{t} (x)$ 难以直接获取，因此 score 也无法直接计算，需通过最小化去噪 score matching 目标来近似：

L = E * x_{0} \sim p_{0}, x_{t} \sim p * t | 0 {| s_{θ} (x, t) - \nabla \log p_{t | 0} (x | x_{0}) |}^{2}

其中， $s_{θ} (x, t)$ 是对 score 的估计，通常由带参数 $θ$ 的神经网络实现。若能较好地最小化 $L$ ，则可逼近真实 score，即 $s_{θ} (x, t) \approx \nabla \log p_{t} (x)$ 。

关键点在于条件分布 $p_{t | 0}$ 通常具备解析形式（而 $p_{t} (x)$ 不具备），因此可用于监督学习。

一旦得到了估计的 score 函数，最常用的采样方式是通过Euler–Maruyama 离散化，将连续 SDE 离散为以下形式：

\begin{matrix} (3) & x_{t - δ} = x_{t} + δ [f (x, t) - g (t)^{2} s_{θ} (x, t)] + g (t) \sqrt{δ} \cdot z, z \sim N (0, I_{d}) \end{matrix}

采样从 $t = 1$ （高斯噪声）开始，按上述式子逐步迭代至 $t = 0$ 。为获得良好生成效果，通常需设置较大的步数 $N \approx 1000$ 。因此，score 函数 $s_{θ}$ 的调用次数成为扩散模型最大的计算瓶颈之一。但已有多个工作尝试减少所需步数 $N$ 。

扩散模型的核心组成要素包括：

(i) 来自目标分布 $p_{0}$ 的数据样本；
(ii) 条件分布 $p_{t | 0}$ 及其可解析的 score；
(iii) 用于估计 score 的神经网络 $s_{θ}$ 。

对条件分布要求解析形式的这一限制，使得扩散过程在扩展至新任务时受限。例如，当先验分布不是高斯时，整个建模方式需重新推导。

为解决这一限制，Flow Matching（FM） 方法被提出。FM 不再依赖 SDE，而是基于无随机性的 ODE，从而允许使用非高斯先验分布，且在性能上与扩散模型相当。

最后，Stochastic Interpolants 提供了一个统一框架，将扩散模型与 Flow Matching 模型联系起来，有助于进一步理解两者在 ODE 与 SDE 建模上的权衡关系。

图 3 | 一维情况下 ODE 与 SDE 轨迹的可视化。左图为仅包含漂移项、未加入噪声的 ODE 轨迹；右图为包含扩散项噪声的 SDE 轨迹，其在跟随漂移的同时叠加了噪声扰动。

2.2 | 几何扩散模型（Geometric Diffusion Models）

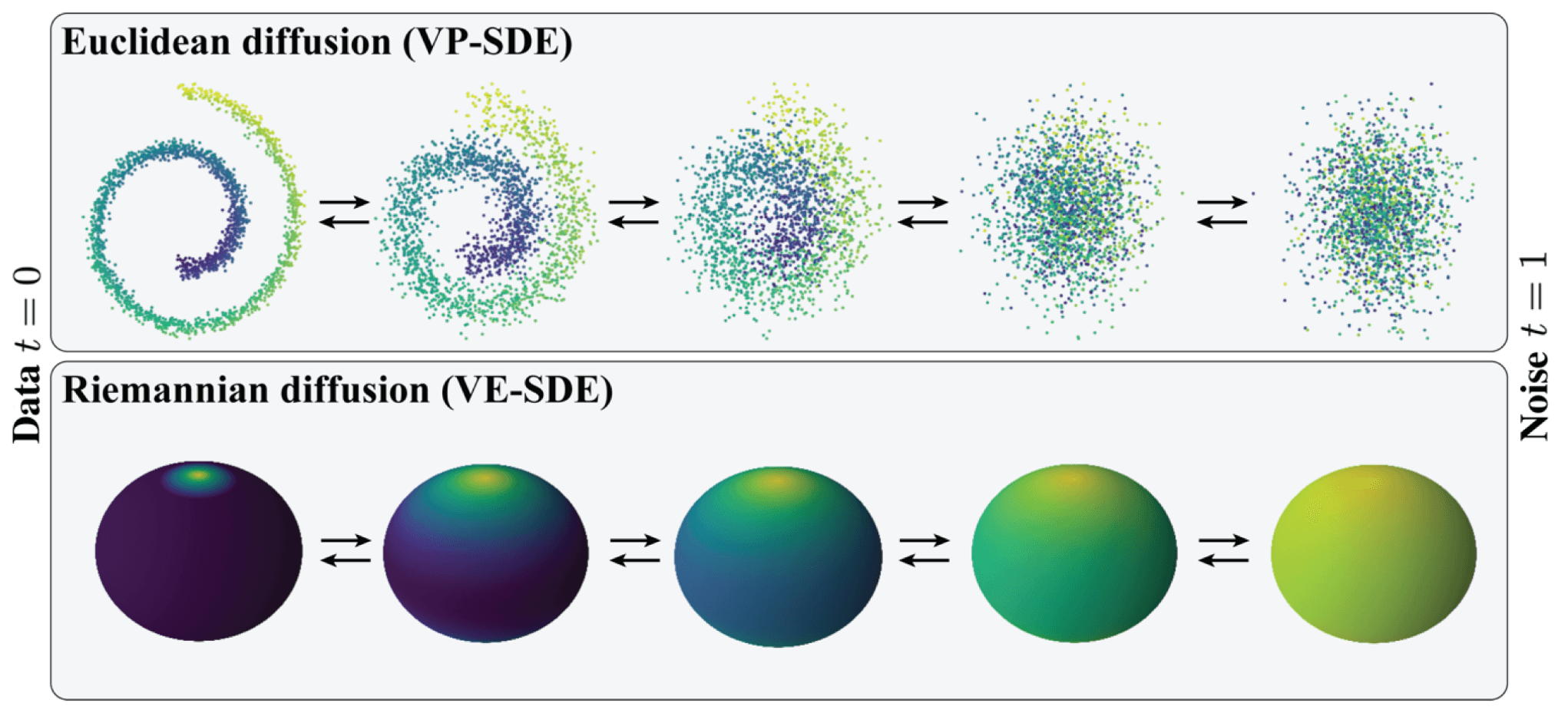
扩散模型在结构生物学中处理的对象多为几何数据，因此有必要进一步探讨其在几何空间中的拓展形式。将几何信息引入扩散模型有助于提升其泛化能力与性能表现。目前几乎所有相关方法都编码了某种对称性（symmetry），其中表现最优的模型通常使用**黎曼流形（Riemannian manifolds）**作为建模空间。以下章节将介绍如何将不变性（invariance）引入扩散模型，并将扩散建模从欧几里得空间推广到非欧几里得空间。

2.2.1 | 三维数据中的不变性（Invariances for 3D data）

不变性是指系统在施加特定变换后，其物理与化学性质保持不变。在结构生物学中，蛋白质与配体的功能依赖于相对距离与成键关系，因此希望模型能够遵循这些不变性，尤其是对 三维空间的旋转与平移不变（SE(3) 不变性）。

设一个变换 $T = (R, υ) \in S E (3)$ ，其中 $R \in S O (3)$ 表示三维旋转矩阵， $υ \in R^{3}$ 为平移向量。设分子系统中 $n$ 个原子的三维坐标为 $x \in R^{3 n}$ ，则变换 $T$ 对 $x$ 的作用为：

T (x) = {R x_{i} + υ}_{i = 1}^{n}, x_{i} \in R^{3}

希望扩散模型满足 SE(3) 不变性，即 $p (T x) = p (x)$ ，表示模型对 $T (x)$ 与 $x$ 赋予相同的概率。

实现路径如下：

平移不变性通过将所有样本进行**质心归零处理（zero-centering）**实现，即在训练阶段对先验分布 $x_{1} \sim p_{1}$ 与数据分布 $x_{0} \sim p_{0}$ 的每个样本都减去其质心：
$COM = \frac{1}{n} \sum_{i = 1}^{n} x_{i}$
在采样阶段，所有中间状态 $x_{t}$ 也保持质心归零。由此，所有生成样本都满足平移不变性。
旋转不变性需构建 SO(3) 不变分布，即 $p (R x) = p (x)$ ，任何旋转版本的 $x$ 具有相同的概率。

扩散模型若满足以下两个条件，即可实现 SO(3) 不变性：
- Score 函数 $s_{θ} (x, t)$ 具备 SO(3) 等变性（equivariance），即 $R s_{θ} (x, t) = s_{θ} (R x, t)$ ；
- 先验分布 $p_{1}$ 本身为 SO(3) 不变，例如各向同性高斯分布（isotropic Gaussian）。
为此，需要选择等变神经网络（equivariant neural networks）进行 score 学习，典型代表包括 AlphaFold2 中的 Invariant Point Attention (IPA) 和 Equivariant Graph Neural Networks (EGNN)。关于更多架构的综述可参考 Joshi 等人的工作。

2.2.2 | 黎曼扩散模型（Riemannian Diffusion Models）

生物分子的三维结构可用三维原子坐标、内部坐标（角度）或两者结合表示。使用内部坐标建模可显著降低维度，有助于提升建模效率。但当建模空间不再是欧几里得空间时，需要将扩散模型推广至黎曼流形（Riemannian Manifolds）。

流形是一类受约束的数学空间，例如：

二维旋转可以用 $[0, 2 π]$ 的角度表示（即 $S O (2)$ ）；
三维旋转表示为 $3 \times 3$ 的正定旋转矩阵（即 $S O (3)$ ）；

与欧几里得空间相比，在流形上进行微积分操作受限，因此需引入切空间（tangent space），它是流形在某点上的局部线性近似，使得可以在其上进行微分、加法等操作。

扩散建模的关键仍然是通过最小化去噪 score matching 损失函数 $L$ ，来近似：

s_{θ} (x, t) \approx \nabla \log p_{t | 0} (x | x_{0})

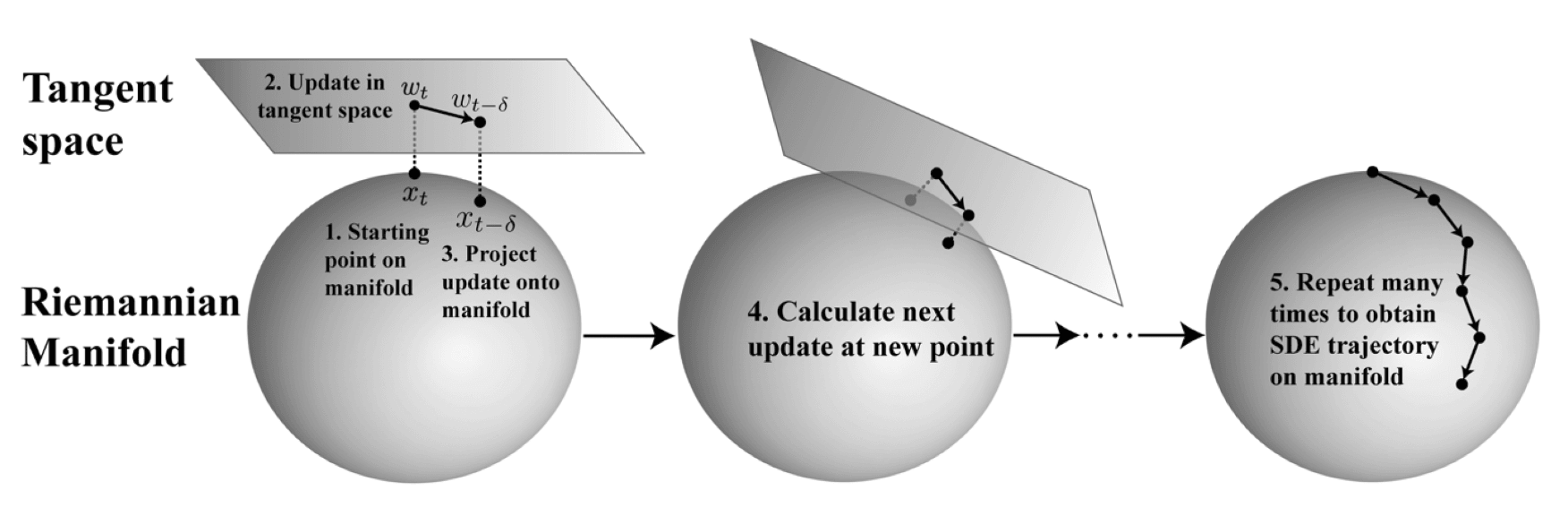
此处的 score 需在切空间上进行计算。图 4 展示了在黎曼流形上进行 SDE 轨迹建模的过程。基本思想是：

在当前点的切空间中更新位置（在该空间内可以使用欧几里得运算）；
然后将更新后的点投影回原始流形，该过程称为指数映射（exponential map）；
此过程可视为在切空间中进行欧几里得扩散建模，并在每一步都重新施加流形的约束。

这一采样过程被称为测地随机游走（Geodesic Random Walk, GRW），是模拟黎曼流形扩散最常用的方法。其核心是使用 Euler–Maruyama 步长（式 3）在切空间更新，然后通过指数映射返回流形（参考 De Bortoli 等人第 3.3 节的定义）。

虽然模拟 SDE 较为容易，但条件分布 $p_{t | 0}$ 的计算难度较大。好消息是，在**紧流形（如球面）**上， $p_{t | 0}$ 通常可被很好地近似并具备解析形式，可用于求导计算 score。随着 $t \to 1$ ，该分布趋于“扩散”至纯噪声状态。图 5 展示了该分布在欧几里得与黎曼空间中的形态变化。

更多 score 学习方法与近似形式可见 De Bortoli 等人论文中的表 2。

然而，对解析形式的依赖限制了扩散模型在一般流形上的适用性。为此，Flow Matching 方法已被扩展至黎曼流形上，有效解决了这一问题。

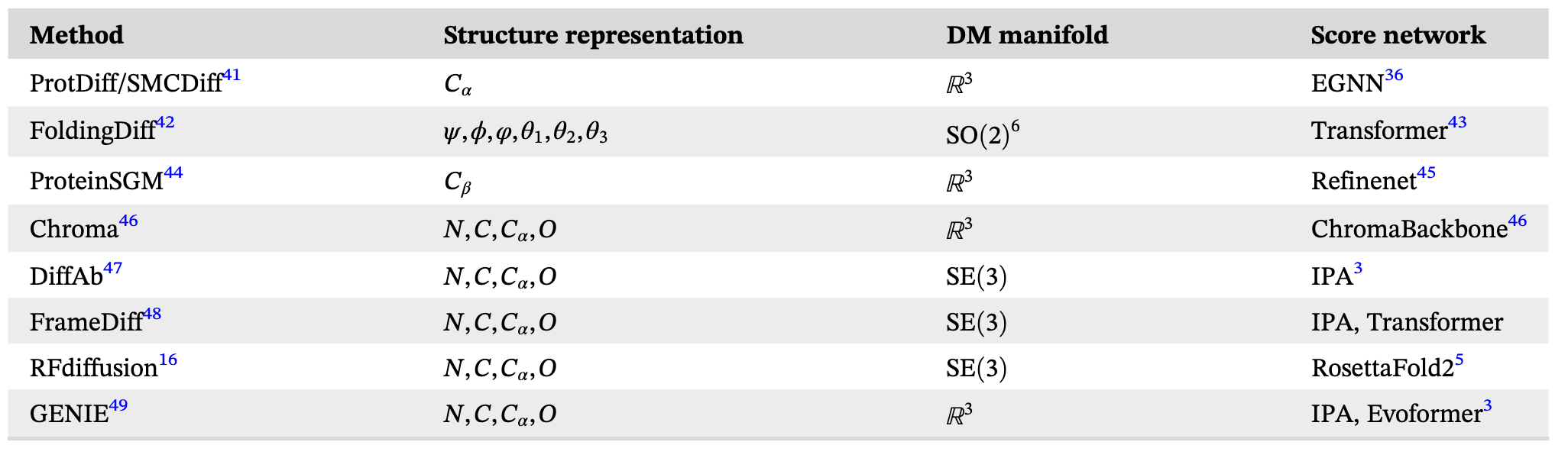
作为总结，表 1 总结了用于三维分子数据的主要黎曼流形类型，并给出了相关方法的实现参考。

图 4 | 展示了在黎曼流形上利用切空间（tangent space）模拟随机微分方程（SDE）轨迹的过程。该过程如下：(1) 在流形上的起始点建立一个切空间；(2) 在切空间中进行更新操作。切空间是欧几里得空间，可以方便地执行加法与微分运算，例如计算 score 并使用公式 (3) 计算下一个点；(3) 将下一个点从切空间投影回原始流形；(4) 与 (5) 重复步骤 1–3 多次，从而在流形上模拟出一条 SDE 轨迹。上述步骤构成了一个测地随机游走（Geodesic Random Walk, GRW）的实例，这是一种在黎曼流形上执行扩散的常见方法。

图 5 | 展示了扩散模型（DMs）在不同几何空间中的应用差异。大多数扩散模型是为欧几里得空间（即实数空间，图上方）设计的。而黎曼扩散模型（Riemannian DMs）则实现了对非欧几里得空间，更一般地说，是对黎曼流形的泛化。这类扩散过程需要额外的几何技术来确保数据始终保持在流形上（图下方）。

表 1 | 不同扩散模型中用于生物分子三维数据的流形类型总结。

表 2 | 蛋白质主链生成中各类扩散模型方法的总结。

图 6 | 展示了自洽性（self-consistency）流程图：主链样本首先经过序列设计，随后进行结构预测。最终将生成结构与预测结构进行比较，其相似性即为自洽性得分（self-consistency score）。

3 | 应用

3.1 | 蛋白质主链生成

蛋白质结构的特征在于其一级结构，即由氨基酸残基组成的线性链条，这决定了蛋白质的三维结构。由于PDB（蛋白质数据银行）中蛋白质结构数据的局限性，蛋白质折叠的研究长期以来主要集中于预测静态结构或最低能量状态。目前，研究的重点正逐步转向利用生成模型来设计新型蛋白质结构，并有条件地生成用于多种应用的结构。

3.1.1 | 评估指标

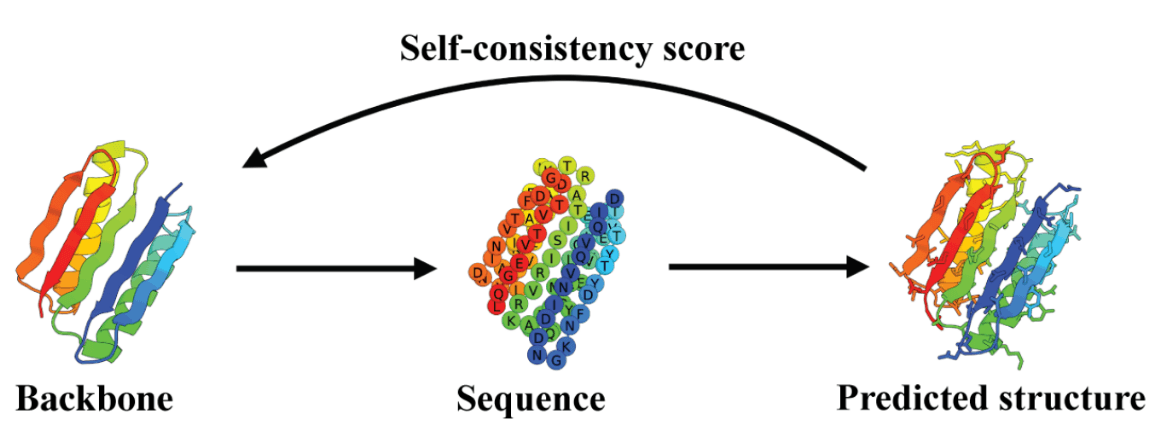
一种常见的评估蛋白质结构样本的方法是，检查一个单独训练的蛋白质结构预测网络是否能够重构生成的结构。这个流程被称为自洽性（self-consistency），如图6所示。

从一个待评估的采样骨架结构开始，需要使用从骨架到序列的生成方法来生成对应的氨基酸序列；这一环节的标准工具是 ProteinMPNN。随后，将生成的序列输入到结构预测网络中（不使用多序列比对）。结构预测网络常用的选择有 AlphaFold2（AF2） 和 ESMFold，其中后者因使用方便而被推荐，尽管准确性可能稍逊一筹。

最后，将预测出的结构与原始骨架样本进行比较，使用的度量包括 TM-score 或 主链原子均方根偏差（RMSD）。我们用 scRMSD 和 scTM 分别表示自洽性流程结束时的 RMSD 和 TM-score。如果一个骨架满足 scTM > 0.5 或 scRMSD < 2.0 Å，就被认为是“可设计的（designable）”。

然而，Watson 等人认为，scTM > 0.5 这个阈值对于原子级精度而言过于宽松。尽管早期研究常用 scTM，我们更推荐使用基于 scRMSD 的指标。此前的研究提供了大量证据表明，以下自洽性评估流程——使用 ProteinMPNN 进行序列设计、使用 AF2 进行结构预测、并满足 scRMSD < 2.0 Å ——在判断蛋白质设计是否能在湿实验室中成功具有良好效果。

“可设计性”通常通过通过 scRMSD（或 scTM）标准的样本比例来报告。

自洽性评估的局限性：

不适用于设计蛋白质-蛋白质相互作用或多聚体，因为多聚体结构预测能力仍存在不足。
不能解释为何某些样本未能通过设计性标准。
目前尚未有系统的研究来分析自洽性评估中的假阳性或假阴性。
某些方法可能通过反复生成相同结构来“利用”自洽性流程。

因此，报告生成样本的多样性也非常重要。常见方法是进行结构聚类，然后报告不同结构簇的数量。

为了评估方法在训练数据以外的泛化能力，可以通过如下方式衡量样本的新颖性：对比样本与 PDB 或 AF2 数据库中长度相同的结构，在全局对齐后计算最小 RMSD 或最大 TM-score。由于 RMSD 要求蛋白质长度相同，TM-score 更常用，因为它支持不同长度蛋白质之间的对齐。

一种常用于快速进行多样性与新颖性计算的工具是 Foldseek。

图7 | 蛋白质主链的简化示意图，它可以被描述为由残基组成的线性链条。每个编号为 i 的残基包含主链中的氮原子（N）、中心碳原子（Cα）、碳原子（C）和氧原子（O）；侧链原子被省略，除非是 ProteinSGM 方法中使用的 Cβ 碳原子。相邻原子之间的共价键的内部坐标由 φ、ψ、φ、θ₁、θ₂、θ₃ 表示。不同方法选择不同的主链表示方式——每种表示方式都有其优势与不足。

3.1.2 | 无条件的骨架生成（Unconditional Backbone Generation）

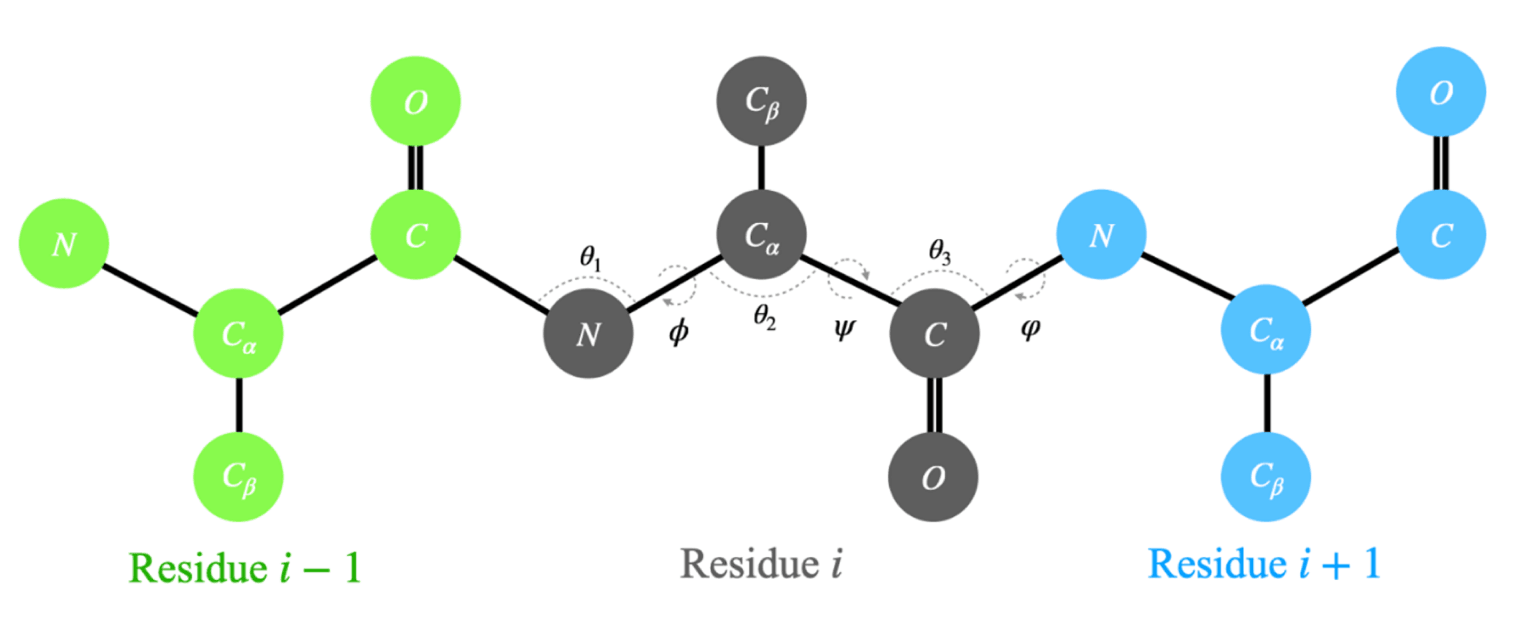
蛋白质结构可以用不同分辨率的层次来表示。目前，大多数扩散模型（DM）仅生成如图7所示的主链原子，而氨基酸序列及其侧链原子则在后续步骤中确定。最粗略的表示方法是仅对每个残基的 Cα 原子 进行建模。

ProtDiff 是一个仅建模 Cα 原子的扩散模型。该方法使用 ProteinMPNN 设计序列，并用 AlphaFold2 (AF2) 补全剩余的原子结构。其主要局限在于容易生成具有**错误手性（chirality）**的结构。由于 ProtDiff 是一个 E(3) 等变模型，它无法区分来源于手性的左旋与右旋螺旋。

为了克服 Cα 建模的局限，ProteinSGM 不再直接建模 Cα，而是扩散 Cβ 原子的成对距离与角度矩阵，但仍需借助 Rosetta 软件来生成三维坐标。

随着表示方法变得更加细致，研究开始尝试生成所有主链重原子（即 N、Cα、C 和 O），并取得显著进展。

例如：

Chroma 构建了一个在欧几里得空间中进行扩散的模型，针对主链原子，并依据蛋白质几何进行理想协方差建模。
FoldingDiff 则扩散二面角和键角，再将其转换为主链坐标进行采样。

另一种方式是将每个残基的重原子表示为一个刚体框架（frame），该框架由三重原子（N, Cα, C）定义，可通过 Gram-Schmidt 正交化过程 计算出位移向量 x（由 Cα 坐标确定）与旋转矩阵 R，从而将每个残基的 (x, R) 映射为 SE(3) 群的元素。

羧基上的 羰基氧原子 对于建模二级结构至关重要。但由于骨架具有一定刚性，只要生成其余主链重原子后，氧原子可以高精度地推断出来，因此不必显式采样。

一些代表性研究：

Anand 等人 在 Cα 上进行欧几里得扩散，并使用 SLERP（球面线性插值）在随机采样旋转和框架旋转之间插值。但其代码未公开，因此该方法在本文后续中被省略。
DiffAb 是较早期使用启发式方法建模框架的扩散模型。
FrameDiff 和 RFdiffusion 则提出了更系统的 SE(3) 扩散方法（参见第2.2.2节）用于建模蛋白质主链。
- FrameDiff 从随机初始化权重开始训练，使用了混合的 IPA3 + Transformer 架构。
- RFdiffusion 则基于预训练的 RosettaFold5 权重，其预训练数据来自蛋白质折叠任务。
- 两者均使用辅助损失函数和**自调节（self-conditioning）**策略。
- RFdiffusion 使用的是 SE(3) 空间中的 Frobenius 范数损失函数，实践中表现更佳。

在无条件蛋白质主链生成任务中，RFdiffusion 在设计性指标上达到了最先进的水平，其预训练策略是关键因素之一。

另一种策略来自 GENIE：它仅在 Cα 坐标上进行欧几里得扩散，但保留了框架表示，通过连续残基的三元 Cα 原子计算旋转矩阵。

关于不同方法中使用的蛋白质结构表示（在扩散模型与评分网络中），可以参考表2。

目前，大多数方法仍依赖后处理步骤来设计序列，有时还包括侧链。开发一个能够同时生成序列和骨架的扩散模型（即协同设计，co-design）有望带来更好的性能和更快的生成速度。

已有一些初步工作正在探索协同设计：

ProteinGenerator 正尝试通过使用序列指导结构生成，并引入基于序列的分类器。
更进一步，生成模型可尝试同时生成骨架、序列和侧链，从而使其支持原子级别的相互作用建模，以用于结合和反应设计。

这方面的初步研究包括：

Protpardelle
RosettaFoldAllAtomDiffusion

图8 | 蛋白质设计任务概览：左上角：一种常见的任务是在与另一种蛋白质结合的条件下进行结构生成。右上角：通过二维距离约束（可视化为一个矩阵）指定一个特定的蛋白质折叠结构，模型在生成过程中需遵守这些约束。左下角：指定一个对称类别（图中为 C10 对称），模型需在该对称性下生成多链复合物。右下角：提供一个被称为motif（功能基序）的残基子集作为条件信息，模型需据此生成其余部分的蛋白质结构，称为scaffold（支架），用于承载该 motif。

3.1.3 | 条件骨架生成（Conditional Backbone Generation）

虽然在无条件的骨架生成方面，尤其是借助框架表示取得了显著进展，但这些模型的实用性很大程度上取决于其执行条件生成的能力。实际上，如图8所示，蛋白质设计本身就是条件生成的直接应用。然而，目前在无条件生成中提到的方法中，只有少数能够进行条件生成。以下是几种重要的条件生成任务的简要介绍：

Motif-Scaffolding（功能基序支架设计）

一种常见情境是给定一组具有特定功能的残基（称为 motif，基序），并设计其余部分的蛋白质（称为 scaffold，支架）来承载该基序【注：常见于酶活性位点设计】。

在扩散模型出现之前，该任务的成功率较低，且难以获得多样化的支架。

若基序的 scRMSD < 1.0 Å，表示基序保持结构完整；
若支架部分 scRMSD < 2.0 Å，表示该支架是可设计的。

SMCDiff 是首个用于该任务的扩散模型，它利用一个预训练的无条件生成模型结合 顺序蒙特卡洛（SMC）方法，在不进行额外训练的情况下构建小型基序的支架。然而，由于所用的 ProtDiff 模型存在局限，效果不佳。

后来，SMCDiff 融合 SMC 扭转（twisting）技术 和更强大的 FrameDiff 生成器，大幅提升了成功率。

ProteinSGM 通过距离输入对基序进行条件建模。
RFdiffusion 在训练时显式输入基序的序列与结构，并仅对支架部分进行扩散建模。
此外，RFdiffusion 引入了一个涵盖多个关键基序的标准测试集，涵盖此前工作的成果，并在单链蛋白主链训练之后，进一步微调以支持酶活性位点的支架设计。

Binder Design（结合蛋白设计）

Motif-scaffolding 假设 motif 和 scaffold 在同一条链上，而 结合蛋白设计 是指设计一个蛋白质以结合另一个目标蛋白（即分子对接设计）。

设计新型结合蛋白或改造已有结合蛋白是生物医学中的关键问题。

DiffAb 通过对目标抗原进行条件建模，从而生成具有更强结合亲和力的抗体 CDR 环。
RFdiffusion 和 Chroma 可通过在训练过程中使用目标蛋白作为条件来生成新的结合蛋白结构。
RFdiffusion 在初始训练后进一步微调以适应蛋白–蛋白相互作用数据，从而支持结合蛋白设计。

对称性设计（Symmetric Design）

大多数天然蛋白质复合物演化出某种点群对称性。

使用小的子单元组装成更大结构，有助于增强灵活性和结构稳定性，这在基因递送系统与疫苗设计中极为关键。

Chroma 和 RFdiffusion 在其得分网络与初始噪声中引入对称投影操作，使其可以生成

折叠结构约束（Fold Conditioning）

有些蛋白质折叠类型具有高度应用价值，例如 Rossmann-like 结构域，据统计在人类蛋白质组中约占 15%。

折叠结构可通过以下方式作为输入条件提供：

二维距离约束矩阵（RFdiffusion）
文本提示描述（Chroma）

通常，折叠结构约束会与其他条件（如结合设计）结合使用。

虽然这些条件生成任务十分重要，但当前扩散模型的评估仍多集中于无条件生成，因为自洽性评估相对成熟且易于实现。相比之下，条件生成的评估更困难，目前尚缺乏公认的体外指标和标准测试集。

其中的一个例外是 Motif-Scaffolding，因为 RFdiffusion 建立了一套横跨多个基序的基准测试。

目前，RFdiffusion 和 Chroma 是最常用于条件生成的扩散模型，已有多项实验室验证结果支持其有效性。

未来展望：构象生成（Conformation Generation）

蛋白质结构预测网络主要基于X 射线晶体学数据训练，后者通常只能捕捉蛋白质在最低能量态的静态构象。然而，蛋白质实际上是高度动态的，在与其他分子结合与游离之间会经历结构变化。

在蛋白质设计与药物发现中，考虑蛋白质的多个可能构象至关重要。

传统方法如 分子动力学（MD）模拟 可用于模拟蛋白质的动态变化，但速度较慢，不适用于高通量应用。
一些基于进化聚类的深度学习方法已能预测多种构象，但并非生成式。
生成式方法则有潜力利用已有 MD 数据进行原理性建模，并结合先进的采样策略以提升效率。

例如，Boltzmann Generators 是将生成模型与 马尔科夫链蒙特卡洛（MCMC）采样及重加权技术结合的例子，能够高效采样小蛋白的平衡态。

目前已有多个初步研究在探索将扩散模型用于构象生成的可能性。

表3 不同扩散模型（DM）对接方法的假设与设计选择汇总。其中，变量 k、n、m、r、s 分别表示：k：配体的扭转角数量 n：配体原子数量 m：受体（蛋白质）原子数量 r：受体的氨基酸数量 s：受体侧链的扭转角数量

3.2 | 分子对接（Molecular Docking）

分子对接指的是理解小分子和蛋白质在三维空间中如何相互作用。由于大多数药物由与某种蛋白质结合的小分子组成，因此分子对接是药物发现中的核心任务。

在该任务中，输入包括：

一个蛋白质结构的笛卡尔坐标；
一个小分子的分子图（即配体，含有原子类型和化学键信息）。

目标是预测配体原子的三维坐标，即它们与蛋白质结合的位置。

传统方法与扩散模型的突破

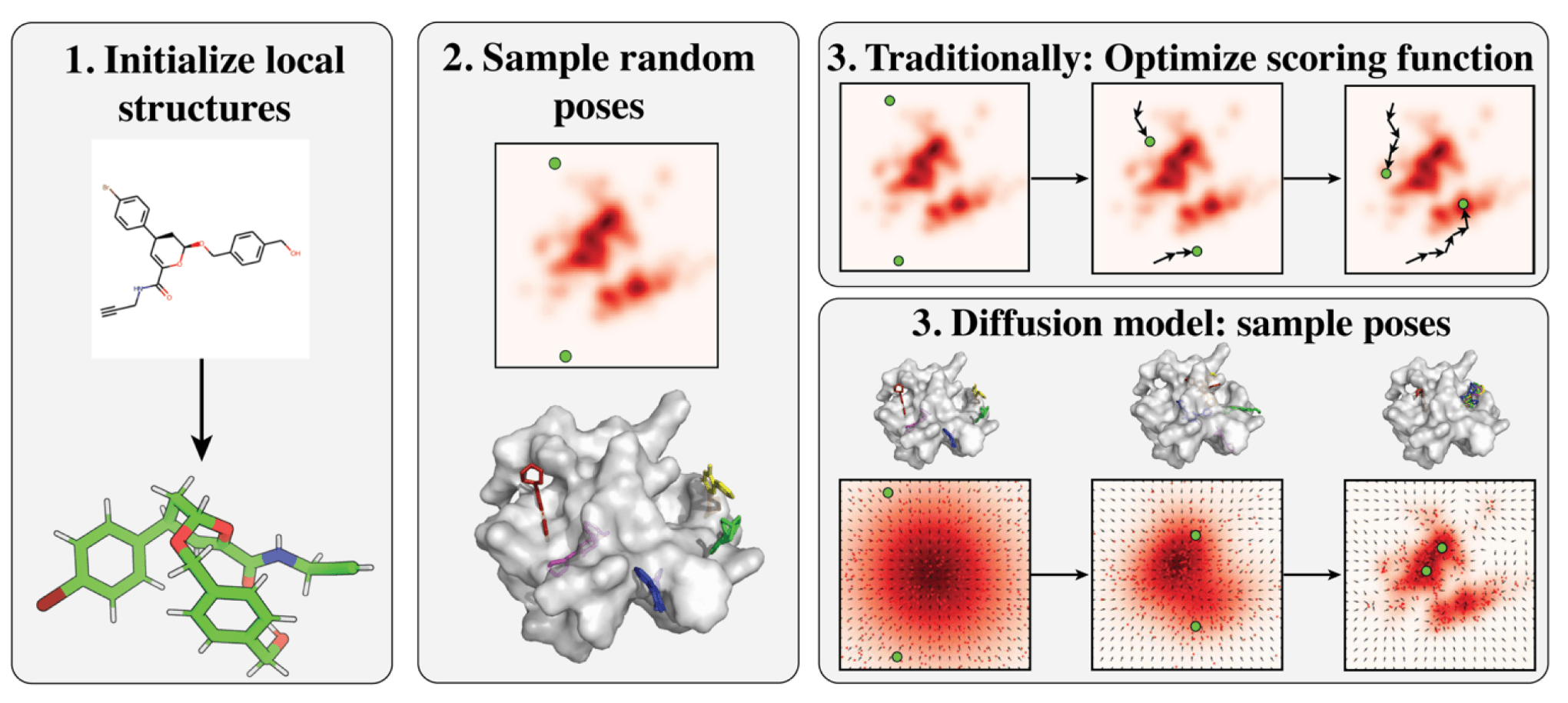
传统方法多采用搜索优化范式，通过各种优化算法在可能的构象空间中搜索，并使用打分函数衡量每种结合构象的合理性【如 AutoDock 等】。

最初的深度学习尝试使用非生成模型直接预测对接构象，以减少计算开销，但效果往往不如传统方法。

DiffDock 提出这些方法表现较差的主要原因是其使用的回归目标函数不合适。

此后，**扩散模型（DM）**开始在机器学习驱动的对接方法中占据主导地位。

不同任务设定与设计假设

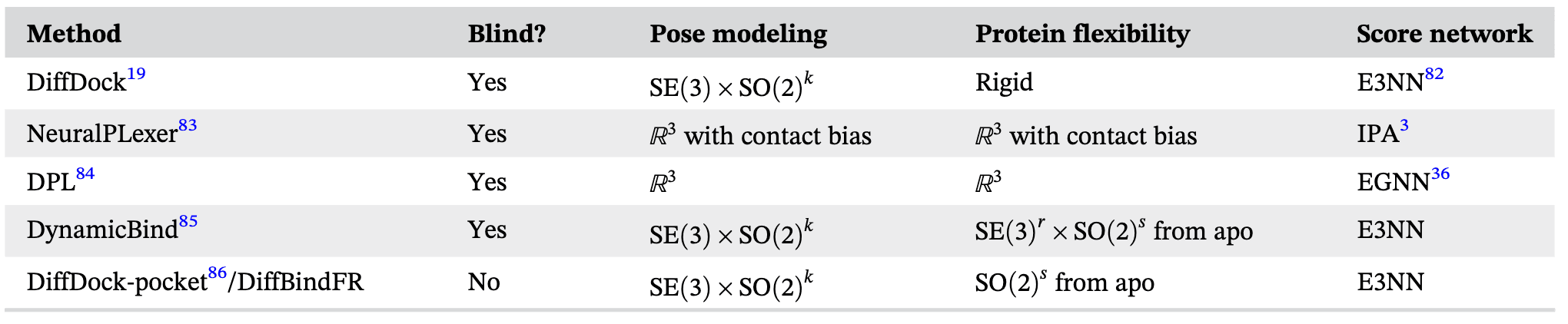
由于应用场景不同，对接任务存在多种变体，对可用先验信息的假设也有所不同。研究者在基于扩散模型的对接中提出了不同的策略以限制搜索空间。以下列出了一些关键设计选择和假设（详见表3）：

盲对接（Blind docking）：对配体结合位点（即“口袋”）一无所知的情况下进行对接。
靶点对接（Pocket-based docking）：事先已知蛋白质中配体结合口袋的位置。

靶点对接在药物发现中较为常见。方法学上，两者在技术实现上的差异通常不大，主要区别在于是否将得分模型的关注区域限制在给定口袋内。

问题：目前并没有统一的“口袋”定义，使得方法间的直接对比困难。有的工作用固定大小的立方体或球体包围真实配体构象作为口袋，有的则将口袋定义为与配体有相互作用的残基集合。

构象生成（Pose Generation）

对接中最关键的是确定配体的三维构象与相对蛋白的位置（统称为 ligand pose）。

主流策略包括：

直接建模原子的三维坐标；
将构象空间限制为扭转角变化 + 刚体变换的组合（反映配体的柔性自由度）。

蛋白质柔性（Protein Flexibility）

由于大多数配体只引起蛋白质结构轻微变化，多数对接方法假设蛋白质为刚性。然而，这使得这些方法无法适应蛋白质结构灵活或未知的情境。

部分扩散模型对接方法已开发出机制将蛋白质柔性纳入搜索空间中。

得分模型架构（Score Model Architecture）

由于模型运行在三维结构空间中，得分网络需具有对原子坐标的 SE(3) 等变性。常见的三类实现策略包括：

不变特征图神经网络（GNN），如 EGNN；
张量积卷积神经网络，如 E3NN 框架；
不变点注意力机制，如 AlphaFold2 的架构。

3.2.2 | 评估方式（Evaluation）

对接预测的价值在于其后续应用，例如用于后续的结合亲和力计算，或帮助科学家理解小分子如何与蛋白结合，并加以优化。

因此，评估标准应以是否对下游任务有用为准：

通常采用的几何评估指标是预测构象与真实构象的 RMSD；
RMSD < 2 Å 是小分子对接中常用的准确性阈值。

此外，构象还必须物理合理，即不能出现立体冲突或高能不稳定状态。

工具如 PoseBusters 提供了这一类物理检查。

数据集与泛化评估

最常用的数据集是 PDBBind，它是从 PDB 精选出的约 20,000 个蛋白–配体复合物。
多项研究在 PDBBind 上基于时间划分进行训练和测试，但测试集中的蛋白质和配体与训练集中高度相似，泛化能力存疑。

为此，建议使用：

基于蛋白质序列相似度或口袋结构相似度的划分；
更大规模的训练集，如使用 PDB 中所有复合物数据，而不仅限于 PDBBind、BindingMOAD、CrossDocked 等子集。

图9 | 小分子构象的更新在构象子流形（pose manifold）对接方法中模拟反向扩散过程时，得分模型可以直接预测当前配体构象的更新，包括：旋转变化（rotation change）、平移变化（translation change）、扭转角的变化（torsion angle changes）。

图10 | 基于构象子流形扩散的对接方法与传统对接流程的关系初始构象准备：传统方法和扩散方法都首先使用化学信息学工具初始化分子的局部结构；随机构象采样：从初始构象中采样随机姿态（pose）；构象优化方式不同：扩散方法：通过学习得到的得分函数，执行反向扩散过程，直接预测构象更新；传统方法：使用优化算法，在打分函数定义的空间中搜索最小值，该打分函数通常只输出一个标量值。

3.2.3 | 蛋白质–蛋白质对接（Protein–Protein Docking）

当配体本身是另一个蛋白质时，其体积更大，且可以利用更多进化信息进行结构预测。

传统方法（如文献94）和早期的深度学习方法（如 EquiDock）将配体和受体都视为刚性体，这大大限制了它们的适用性，相比之下，AlphaFold Multimer 等折叠方法表现更佳。

同样的问题也适用于 DiffDock-PP 和 Diff-MasIF，它们通过在配体的旋转和平移空间中执行反向扩散来完成对接。

因此，在后续讨论中，我们将重点聚焦于小分子与蛋白质对接。

3.2.4 | 构象生成（Pose Generation）

一个含有 n 个原子的配体，其构象由 3n 个欧几里得坐标描述。可以在该空间上构建扩散生成过程来预测对接构象。

但如同蛋白质结构生成一样，将归纳偏置引入扩散模型、对其建模空间进行限制也被证明是有效的。

一个合理的限制（也为传统对接方法所采用）是：

仅允许配体在扭转角上具备柔性；
化学键信长、键角和环结构保持固定，基于初始结构（通常通过标准化学信息学工具生成）。

该策略最早由 Torsional Diffusion 方法提出于小分子构象生成任务，随后被 DiffDock 应用于对接任务。

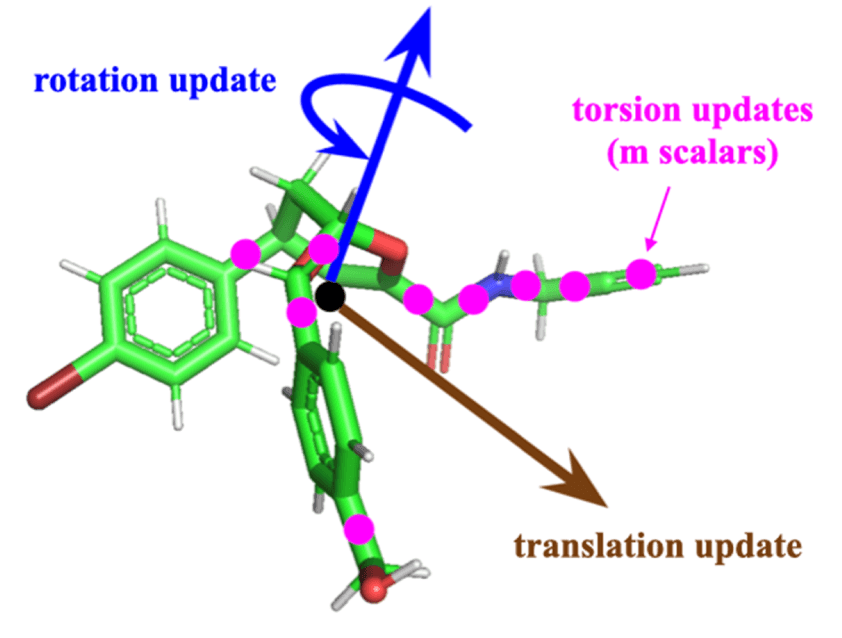
Pose Manifold 表示（构象子流形建模）

DiffDock 将构象建模为一个维度为 k+6 的子流形（pose manifold）上的生成过程，其中：

k 表示配体的扭转角数；
6 表示刚体自由度（3 个平移 + 3 个旋转）。

这个流形在数学上与 SE(3) × SO(2)^k 等同，是一个黎曼流形。

DiffDock 及后续方法采用这种建模方式。

该方法从随机初始化的配体构象出发，逐步预测其扭转角、旋转和平移更新，以逼近最终结合构象（见图9）。

优势与局限

优点：

与传统对接方法概念上相似，工作流程兼容；
保持配体的手性（chirality）；
避免不合理的形变，产生物理合理的构象；
模型稳定，易于解释。

局限：

对于 带有额外柔性 的配体（如大环结构、融合环系统、多肽或糖类分子），处理能力受限；
流形上的建模对 得分模型的架构要求高，操作复杂；
通常需要 更昂贵的运算操作（如 E3NN 的张量积卷积）。

欧几里得建模替代策略

后续的一些研究（如 NeuralPlexer）采用了完全在 欧几里得空间中建模配体柔性的策略，代表了另一种方向。

NeuralPlexer 通过：

更大的训练集、
更深的模型架构、
大规模分子预训练，

在对接成功率上追平甚至超过了基于 pose manifold 的方法。其核心架构采用类似 AF2 的 EvoFormer 和 RoseTTAFold 的 2D 轨道堆叠结构。

随着蛋白质结构预测中的构建模块被引入配体–蛋白建模，欧几里得建模有望因其结构简单、可扩展性强而逐步占据优势。

此外，欧几里得建模的架构更易于扩展，可以通过增加参数量获得更高性能，而不依赖强归纳偏置的模型则面临架构复杂与计算昂贵的问题。

值得一提的是，虽然本文不详细展开，但目前已有一些基于回归的非扩散方法，利用蛋白结构预测模型也在对接任务中展现出优异表现。

3.2.5 | 蛋白质柔性（Protein Flexibility）

蛋白质在未结合状态（unbound）下的三维结构，与其结合后的状态（bound）可能显著不同。

因此，对接问题可以分为两种情境：

刚性蛋白质假设：输入的是已知的结合构象（适用于有高分辨率结构的目标蛋白）；
柔性蛋白质设定：只知道未结合结构或根本没有结构信息，需预测构象变化。

侧链柔性（Side-Chain Flexibility）

在小分子对接中，蛋白质的结构变化大多发生在结合位点附近的侧链。

一种合理的简化是：

固定主链，只允许侧链发生构象变化。

这对于基于口袋的对接尤为适用（如药物发现场景），并对下游的结合自由能计算具有重要意义。

传统方法通过将侧链扭转角加入搜索空间来模拟这种柔性，但这会显著降低搜索效率。

基于此，扩散模型如：

DiffDock-Pocket
DiffBindFR

扩展了 DiffDock 的扩散过程，引入了对侧链扭转角的建模，同时几乎不增加运行时间。

完全柔性蛋白建模（Full Protein Flexibility）

完全建模蛋白构象变化更为复杂，因此在传统方法中使用较少。

DynamicBind 是一个支持完全蛋白柔性的扩散方法：

在未结合蛋白结构上添加噪声；
学习反向扩散过程，将其恢复为结合状态；
同时生成配体构象。

其利用模板蛋白结构的特征作为额外输入，达到对未结合结构的条件建模。

以下是你提供内容的中文翻译：

4 | 结论（Conclusion）

扩散模型（Diffusion Models, DMs） 已经在计算结构生物学领域带来了诸多进展。

它们在生成具有高可设计性、多样性和新颖性的蛋白质结构方面表现优异，超越了 PDB 数据库中已知结构的限制。

这些模型的优势，部分源于其能够将几何信息有效地整合进强大的深度学习架构中。

本综述主要从蛋白质主链生成的角度探讨了扩散模型，包括无条件生成与条件生成两类任务。

一个自然的问题是：

是否将主链、氨基酸序列与侧链进行联合建模（而非依次建模）会带来更大优势？

作者的猜想是：会的。

这将依赖于更强的全原子神经网络架构以及对全原子数据的更高效利用。

未来更准确的蛋白质相互作用预测方法也将推动对生成能力的高质量体内（in silico）评估，进一步支持研究人员严谨地验证新方法的有效性。

此外，扩散模型也在重塑分子对接等传统任务，使得诸如盲对接、柔性对接等以往几乎无法解决的问题变得可行。

尽管如此，目前仍存在一些关键限制，例如：

结合位点精度的提升仍有待改进；
对新受体和新化合物的泛化能力仍需增强。

扩散模型是否会经受住时间的考验？

目前，机器学习领域正积极探索扩展方法，如：

流匹配（Flow Matching）
薛定谔桥（Schrödinger Bridges）
随机插值（Stochastic Interpolants）

这些改进及可能出现的全新生成范式，有望在前述应用中带来真正的突破。

我们相信，生成式建模方法将持续作为结构生物学核心建模理念之一，发挥重要作用。